Filtering

Now, we are actually building a signal processing pipeline that also processes the data! And fortunately, the Datapipeline API has a ready-to-use component for that, too!
In this example, we are going to generate a 32 channel signal with different frequencies per channel. And we are also going to add some random noise to it. Before plotting we are also going to process -- bandpass filtering -- the signal.
 

import RZ2ephys
from scipy.signal import butter
def example9():
    aSignalGenerator = pipeline.SignalGenerator()
    duration = 1
    frequency = 1.0
    amplitude = 2.0
    theta = 0.0
    sampleRate = 24414
    numChannels = 32
    nyquist = sampleRate/2  
    b,a = butter(4,(10/nyquist, 500/nyquist),'bandpass')#make filter coefficients for an 10,500 Hz band pass filter
    filterCoefficients = [b,a]
    
    aDatasource = pipeline.Datasource()
    aDatasource.setName("Our Signal Datasource")
    aSweepFiltFiltFilterPlugin = pipeline.SweepFiltFiltFilterPlugin()
    aSweepFiltFiltFilterPlugin.setName("Our SweepFiltFiltFilterPlugin")
    aSweepFiltFiltFilterPlugin.setFilterCoeffs(filterCoefficients)
    aDisplay = pipeline.MplSweepDataDisplay(plt)
    aDisplay.setName("Our Signal DataDisplay")
    aDatasink = pipeline.Datasink()
    aDatasink.setName("Our Signal Datasink")

    aDatasource.setOutput(aSweepFiltFiltFilterPlugin)
    aSweepFiltFiltFilterPlugin.setOutput(aDisplay)
    aDisplay.setOutput(aDatasink)
    
    for n in range(100):
        #generate multichannel data    
        time, signalBuffer = aSignalGenerator.makeNChannelSineWave(duration,frequency,amplitude, theta, sampleRate, numChannels)
        lenOfSignal = len(signalBuffer[0:,0])
        sigChunk=np.zeros(lenOfSignal*numChannels)
        sigTupel = tuple(sigChunk)
        #create MCsweep object
        data=RZ2ephys.MCsweep(sigTupel,lenOfSignal,sampleRate,0)
        for chanIdx in range(numChannels):
            data.signal[0:,chanIdx] = (signalBuffer[0:,chanIdx]+np.random.random(lenOfSignal))*np.random.random(1)
        aDataframe = pipeline.Dataframe()
        aDataframe.setFrameNumber(n)
        aDataframe.setData(data)
        aDatasource.addDataframe(aDataframe)
        aDatasource.run()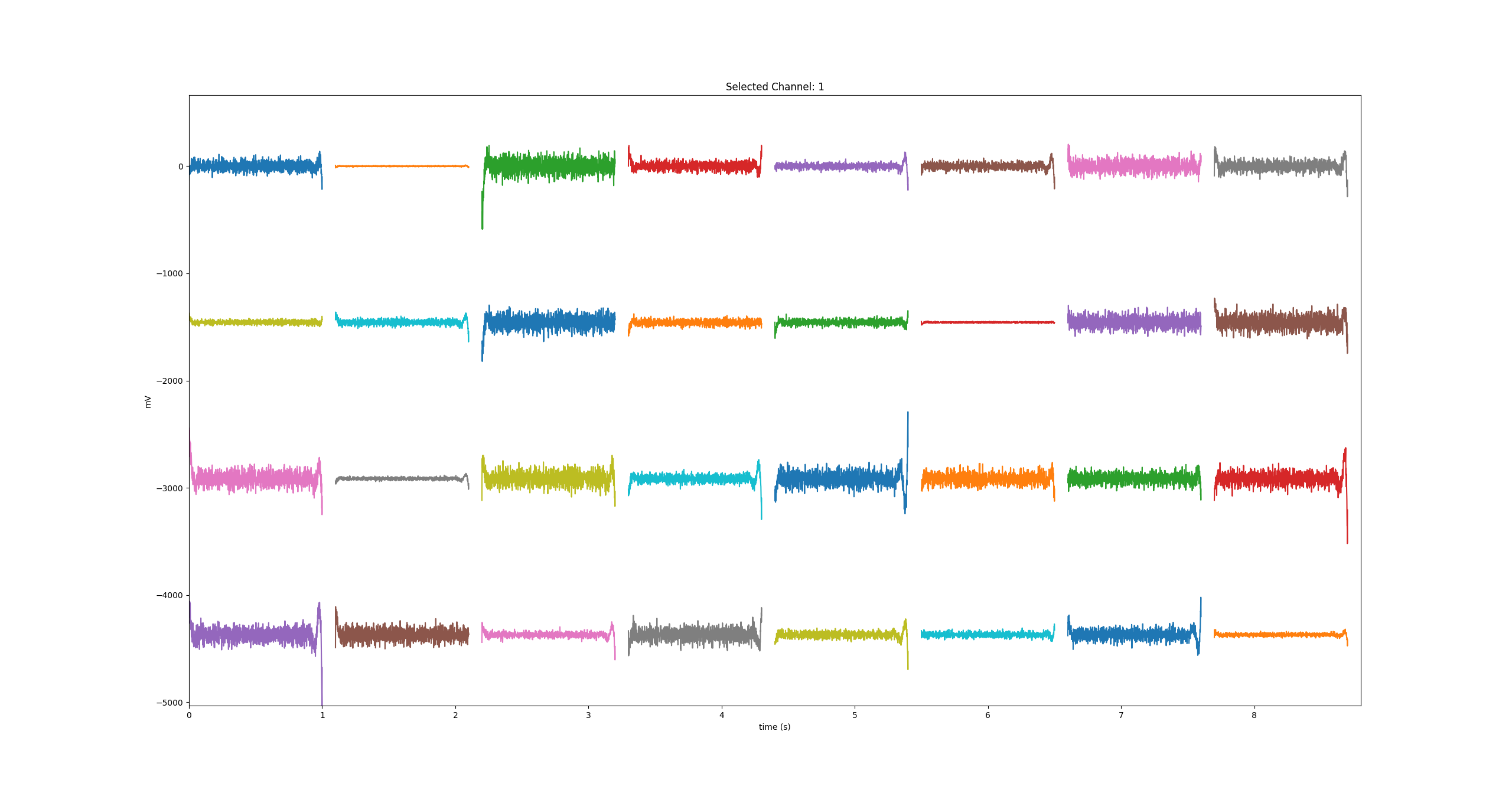

filtered signal
Fig11: This plot shows the bandpass filtered noise-contaminated and amplitude modulated sine wave.

Although the plot looks nice, we cannot see the original signal. Fortunately, we can also plot it. For that, we just have to clone the unfiltered data stream as we have already done it before!

Here is the source code:

import RZ2ephys
from scipy.signal import butter
def example10():
    aSignalGenerator = pipeline.SignalGenerator()
    duration = 1
    frequency = 1.0
    amplitude = 2.0
    theta = 0.0
    sampleRate = 24414
    numChannels = 32
    nyquist = sampleRate/2  
    b,a = butter(4,(10/nyquist, 500/nyquist),'bandpass')#make filter coefficients for an 10,500 Hz band pass filter
    filterCoefficients = [b,a]
    numberOfClones = 2
    
    aDatasource = pipeline.Datasource()
    aCloneDatasource = pipeline.CloneDatasource(numberOfClones)
    aDatasource.setName("Our Signal Datasource")
    aSweepFiltFiltFilterPlugin = pipeline.SweepFiltFiltFilterPlugin()
    aSweepFiltFiltFilterPlugin.setName("Our SweepFiltFiltFilterPlugin")
    aSweepFiltFiltFilterPlugin.setFilterCoeffs(filterCoefficients)
    aDisplay0 = pipeline.MplSweepDataDisplay(plt)
    aDisplay0.setName("Our Signal DataDisplay")
    aDisplay1 = pipeline.MplSweepDataDisplay(plt)
    aDisplay1.setName("Our Signal DataDisplay")
    
    aDatasource.setOutput(aCloneDatasource)
    aCloneDatasource = pipeline.CloneDatasource(numberOfClones)
    aDatasink0 = pipeline.Datasink()
    aDatasink0.setName("Our Signal Datasink")
    aDatasink1 = pipeline.Datasink()
    aDatasink1.setName("Our Signal Datasink")
    
    aDatasource.setOutput(aCloneDatasource)
    aCloneDatasource.setOutput(aDisplay0, 0)
    aDisplay0.setOutput(aDatasink0)
    aCloneDatasource.setOutput(aSweepFiltFiltFilterPlugin, 1)
    aSweepFiltFiltFilterPlugin.setOutput(aDisplay1)
    aDisplay1.setOutput(aDatasink1)
    
    for n in range(100):
        #generate multichannel data    
        time, signalBuffer = aSignalGenerator.makeNChannelSineWave(duration,frequency,amplitude, theta, sampleRate, numChannels)
        lenOfSignal = len(signalBuffer[0:,0])
        sigChunk=np.zeros(lenOfSignal*numChannels)
        sigTupel = tuple(sigChunk)
        #create MCsweep object
        data=RZ2ephys.MCsweep(sigTupel,lenOfSignal,sampleRate,0)
        for chanIdx in range(numChannels):
            data.signal[0:,chanIdx] = (signalBuffer[0:,chanIdx]+np.random.random(lenOfSignal))*np.random.random(1)
        aDataframe = pipeline.Dataframe()
        aDataframe.setFrameNumber(n)
        aDataframe.setData(data)
        aDatasource.addDataframe(aDataframe)
        aDatasource.run()

And this is what the output looks like:

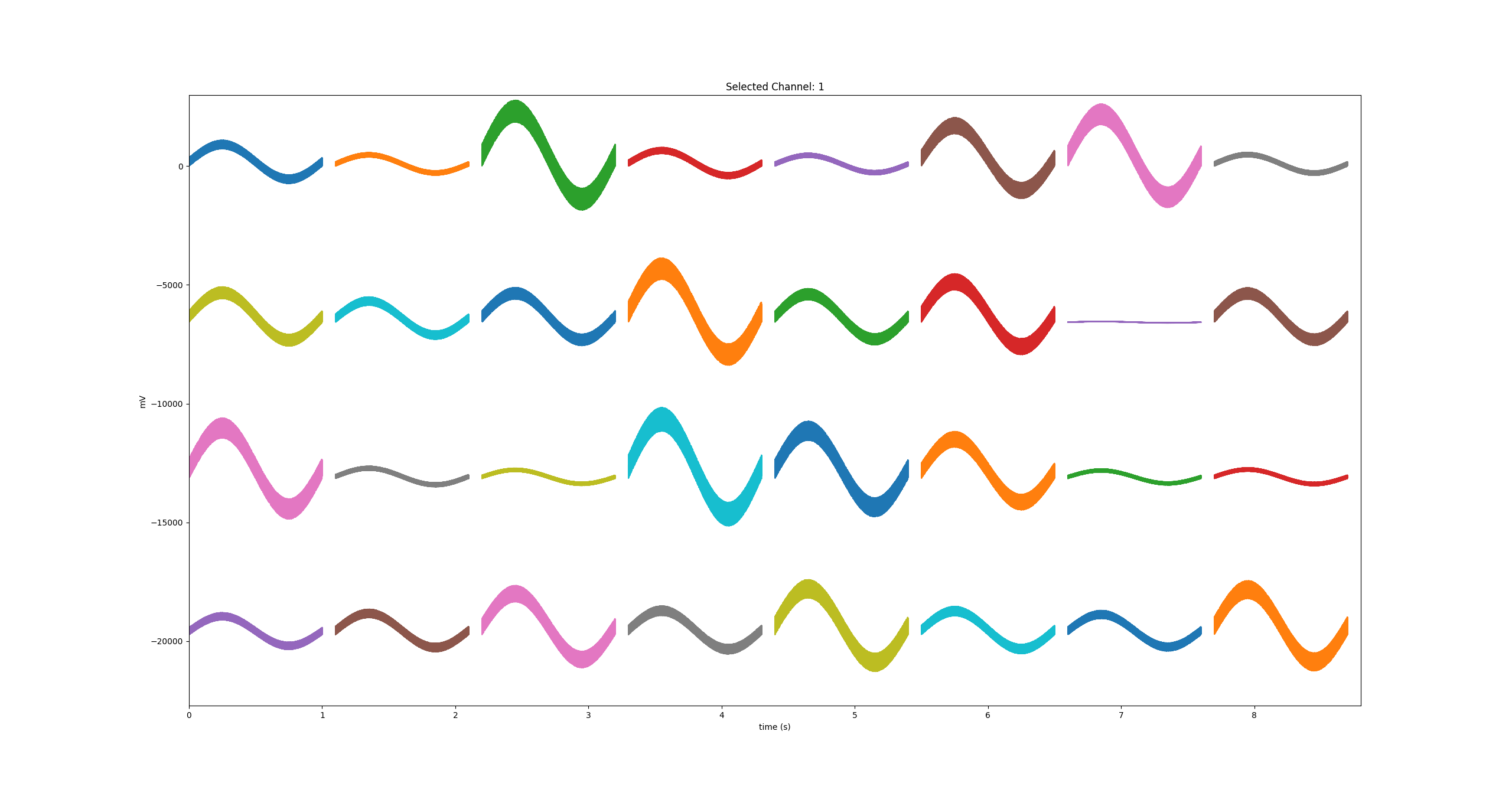
originalSignal
Fig12:This is the unfiltered original signal generated in  example9() and example1()

It is important to realize that the structure of example 10 is essentially identical to example 5. Let's compare:

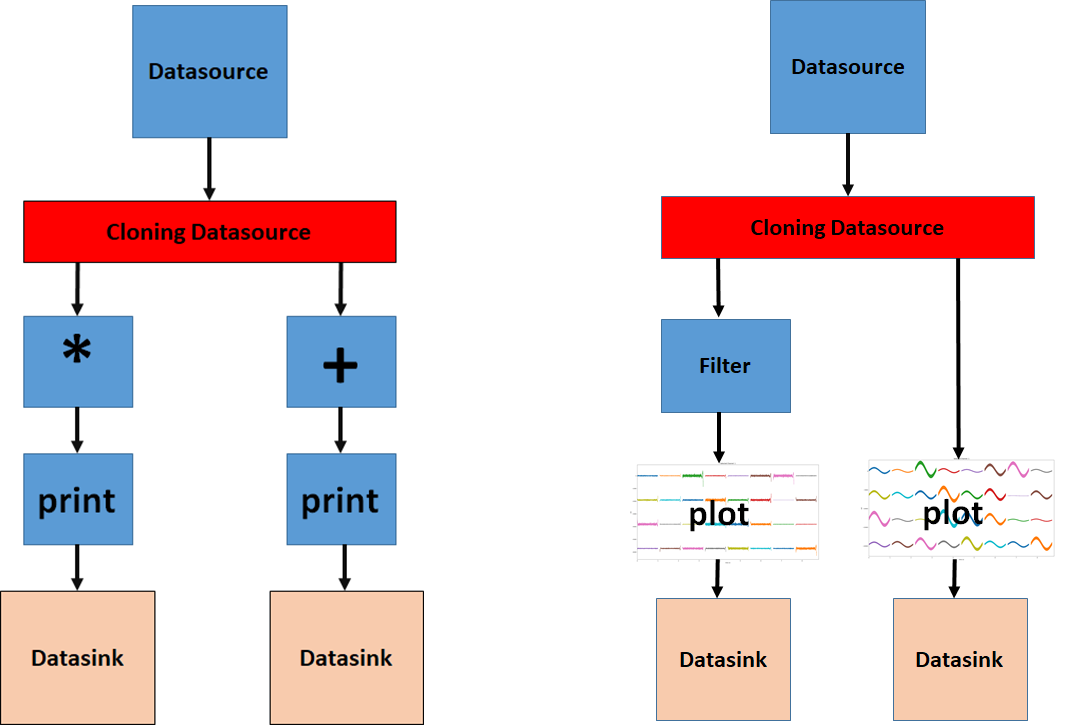
cloning structure
Figure13: On the left, we see the structure of example5 where we have created some random numbers and then cloned this data into two identical data streams. After that, we have multiplied the data with a constant in the left branch, and in the right branch of the pipeline, we have added a constant value. Both results were then visualized by printing them on the screen before sending the data to the datasinks.

The figure on the right side shows the structure of the pipeline that we have just created in example 10. Conceptually, the structure is very similar to example 5. Instead of creating random numbers, we have created multichannel signals which are then cloned to get two identical data streams. The left branch of the pipeline filters the signals and plots the results and then sends the signals to the datasink. The right branch just plots the signals before sending them to the datasink.