6

Auditory Scene Analysis

6.1 What Is Auditory Scene Analysis?

I’m sitting at the doors leading from the kitchen out into a small back garden. I hear the traffic in the nearby main road, and the few cars that turn from the main road into the little alley where the house stands. I hear birds—I can recognize the song of a blackbird. I hear the rustling of the leaves and branches of the bushes surrounding the garden. A light rain starts, increasing in intensity. The raindrops beat on the roofs of the nearby houses and on the windows of the kitchen.

Sounds help us to know our environment. We have already discussed, in some detail, the physical cues we use for that purpose. In previous chapters we discussed the complex processing required to extract the pitch, the phonemic identity (in case of speech), or the spatial location of sounds. However, so far we implicitly assumed that the sounds that need to be processed arise from a single source at any one time. In real life, we frequently encounter multiple sound sources, which are active simultaneously or nearly simultaneously. Although the sound waves from these different sources will arrive at our ears all mixed together, we nevertheless somehow hear them separately—the birds from the cars from the wind in the leaves. This, in a nutshell, is auditory scene analysis.

The term “auditory scene analysis” has been coined by the psychologist Albert Bregman, and popularized through his highly influential book with that title. In parallel with the by now classic studies of auditory scene analysis as a psychoacoustic phenomenon, the field of computational auditory scene analysis has emerged in recent years, which seeks to create practical, computer-based implementations of sound source separation algorithms, and feeds back experience and new insights into the field.

Auditory scene analysis today is not yet a single, well-defined discipline, but rather a collection of questions that have to do with hearing in the presence of multiple sound sources. The basic concept that unifies these questions is the idea that the sounds emitted by each source reflect its distinct properties, and that it is possible to group those elements of the sounds in time and frequency that belong to the same source, while segregating those bits that belong to different sources. Sound elements that have been grouped in this manner are sometimes referred to as an “auditory stream,” or even as an “auditory object.” If auditory scene analysis works as it should, one such stream or object would typically correspond to the sound from a single source. However, “grouping,” “segregation,” “streams,” and “auditory objects" are not rigorously defined terms, and often tested only indirectly, so be aware that different researchers in the field may use these terms to describe a variety of phenomena, and some may even reject the idea that such things exist at all.

In our survey of auditory scene analysis, we will therefore reexamine the idea that we group or segregate sounds, or construct auditory objects under different experimental conditions. We will start with a very simple situation—a pure tone in a background noise—in which different descriptions of auditory scene analysis can be discussed in very concrete settings. Then we will discuss simultaneous segregation—the ability to “hear out” multiple sounds that occur at the same time, and we will discuss the way information about the composition of the auditory scene accumulates with time. Finally, with these issues and pertinent facts fresh in our minds, we will revisit the issues surrounding the existence and nature of auditory objects at the end of the chapter.

6.2 Low- and High-Level Representations of the Auditory Scene: The Case of Masking

One of the classical experiments of psychoacoustics is the measurement of the detection threshold for a pure-tone “target” in the presence of a white noise “masker.” In these experiments, the “target” and the “masker” are very different from each other—pure tones have pitch, while white noise obviously does not. Introspectively, that special quality of the pure tone jumps out at us. This may well be the simplest example of auditory scene analysis: There are two “objects,” the tone and the noise, and as long as the tone is loud enough to exceed the detection threshold, we hear the tone as distinct from the noise (Sound Example "Masking a Tone by Noise" on the book's Web site <flag>). But is this really so?

There is an alternative explanation of masking that doesn’t invoke the concept of auditory scene analysis at all. Instead, it is based on concepts guiding decisions based on noisy data, a field of research often called signal detection theory. The assumptions that are required to apply the theory are sometimes unnatural, leading to the use of the term “ideal observer” with respect to calculations based on this theory. In its simplest form, signal detection theory assumes that you know the characteristics of the signal to detect (e.g., it is a pure tone at a frequency of 1,000 Hz) and you know those of the noise (e.g., it is Gaussian white noise). You are presented with short bits of sounds that consist either of the noise by itself, or of the tone added to the noise. The problem you face consists of the fact that noise by nature fluctuates randomly, and may therefore occasionally slightly resemble, and masquerade as, the pure-tone target, especially when the target is weak. It is your role as a subject to distinguish such random fluctuations from the “real” target sound. Signal detection theory then supplies an optimal test for deciding whether an interval contains only noise or also a tone, and it even makes it possible to predict the optimal performance in situations such as a two-interval, two-alternative forced choice (2I2AFC) experiment, in which one interval consists of noise only and one interval also contains the tone.

How does this work in the case of a tone in white noise? We know (see chapter 2) that the ear filters the signal into different frequency bands, reflected in the activity of auditory nerve fibers that synapse hair cells at different locations along the basilar membrane. The frequency bands that are far from the tone frequency would include only noise. Bands that are close to the tone frequency would include some of the tone energy and some noise energy. It turns out that the optimal decision regarding the presence of the tone can be essentially reached by considering only a single frequency band—the one centered on the tone frequency. This band would include the highest amount of tone energy relative to the noise that goes through it. Within that band, the optimal test is essentially energetic. In a 2I2AFC trial, one simply measures the energy in the band centered on the target tone frequency during the two sound presentations, and “detects” the tone in the interval that had the higher energy in that band. Under standard conditions, no other method gives a better detection rate. In practice, we can imagine these bands evoking activity in auditory nerve fibers, and the optimal performance is achieved by simply choosing the interval that evoked the larger firing rate in the auditory nerve fibers tuned to the signal frequency.

How often would this optimal strategy correctly identify the target interval? This depends, obviously, on the level of the target tone, but performance would also depend in a more subtle way on the bandwidth of the filters. The reason is that, whereas all the energy of the tone would always be reflected in the output of the filter that is centered on the target tone frequency, the amount of noise that would also pass through this filter would be larger or smaller depending on its bandwidth. Thus, the narrower the band, the smaller the contribution of the masking noise to its output, and the more likely the interval with the higher energy would indeed be the one containing the target tone.

This argument can be reversed: Measure the threshold of a tone in broadband noise, and you can deduce the width of the peripheral filter centered at the tone frequency from the threshold. This is done by running the previous paragraph in the reverse—given the noise and tone level, the performance of the ideal observer is calculated for different filter bandwidths, until the calculated performance matches the experimental one. And indeed, it turns out that tone detection thresholds increase with frequency, as expected from the increase in bandwidth of auditory nerve fibers. This argument, originally made by Harvey Fletcher (an engineer in Bell Labs in the first half of the twentieth century), is central to much of modern psychoacoustics. The power of this argument stems from the elegant use it makes of the biology of the early auditory system (peripheral filtering) on the one hand, and of the optimality of signal detection theory on the other. It has been refined to a considerable degree by other researchers, leading to the measurement of the width of the peripheral filters (called “critical bands” in the literature) and even the shape of the peripheral filters (Unoki et al., 2006). The central finding is that, in many masking tasks, human performance is comparable to that calculated from theory, in other words, human performance approaches that of an ideal observer.

However, note that there is no mention of auditory objects, segregation, grouping, or anything else that is related to auditory scene analysis. The problem is posed as a statistical problem—signal in noise—and is solved at a very physical level, by considerations of energy measurements in the output of the peripheral filters. So, do we perform auditory scene analysis when detecting pure tones in noise, or are we merely comparing the output of the peripheral filters, or almost equivalently, firing rates of auditory nerve fibers?

As we shall see, similar questions will recur like a leitmotif throughout this chapter. Note that, for the purpose of signal detection by means of a simple comparison of spike counts, noise and tone “sensations” would seem to be a superfluous extra, nor is there any obvious need for segregation or grouping, or other fancy mechanisms. We could achieve perfect performance in the 2I2AFC test by “listening” only to the output of the correct peripheral frequency channel. However, this does not mean that we cannot also perform segregation and grouping, and form separate perceptual representations of the tone and the noise. Signal detection theory and auditory scene analysis are not mutually exclusive, but, at least in this example, it is not clear what added value scene analysis offers.

We encountered similar issues regarding high-level and low-level representations of sound before: There are physical cues, such as periodicity, formant frequencies, and interaural level differences; and then there are perceptual qualities such as pitch, speech sound identity, and spatial location. We know that we extract the physical cues (in the sense that we can record neural activity that encodes them), but we do not perceive the physical cues directly. Rather, our auditory sensations are based on an integrated representation that takes into account multiple cues, and that, at least introspectively, is not cast in terms of the physical cues—we hear pitch rather than periodicity, vowel identity rather than formant frequencies, and spatial location rather than interaural disparities. In masking, we face a similar situation: performance is essentially determined by energy in peripheral bands, but introspectively we perceive the tone and the noise.

The presence of multiple representation levels is actually congruent with what we know about the auditory system. When discussing pitch, speech, and space, we could describe in substantial details the processing of the relevant parameters by the early auditory system: periodicity enhancement for pitch, measuring binaural disparities or estimating notch frequencies for spatial hearing, estimating formant frequencies of vowels, and so on. On the other hand, the fully integrated percept is most likely represented in cortex, often beyond the primary cortical fields.

Can we experimentally dissociate between low- and high-level representations in a more rigorous way? Merav Ahissar and Shaul Hochstein constructed a conceptual framework, called reverse hierarchy theory (RHT), to account for similar effects in vision (Hochstein & Ahissar, 2002). Recently, Nahum, Nelken, and Ahissar (2008) adapted this framework to the auditory system and demonstrated its validity to audition as well. RHT posits the presence of multiple representation levels, and also the fact (which we have emphasized repeatedly) that consciously, we tend to access the higher representation levels, with their more ecological representation of the sensory input. Furthermore, RHT also posits that the connections between different representation levels are dynamic—there are multiple low-level representations, and under the appropriate conditions we can select the most informative low-level representation for the current task. Finding the most informative low-level representation can, however, take a little while, and may require a search starting at high representation levels and proceeding backward toward the most informative low-level representations. Also, this search can find the best low-level representation only if the stimuli are presented consistently, without any variability except for the task-relevant one.

Classic psychoacoustic experiments, where the tone frequency is fixed, provide optimal conditions for a successful search for the most task-relevant representation, such as the activity of the auditory nerve fibers whose best frequency matches the frequency of the target tone. Once the task-relevant representation is accessed, behavioral performance can reach the theoretical limits set by signal detection theory. Importantly, if the high-level representation accesses the most appropriate low-level representation, the two become equivalent and we then expect a congruence of the conscious, high-level percept with the low-level, statistically limited ideal observer performance.

This theory predicts that ideal observer performance can be achieved only under limited conditions. For example, if the backward search is interrupted, performance will become suboptimal. Nahum et al. (2008) therefore performed a set of experiments whose goal was to disrupt the backward search. To do so, they needed a high-level task that pitted two low-level representations against each other. In chapter 5, we discussed the detection of tones in noise when the tones are presented to the two ears in opposite phase (binaural masking level differences, BMLDs). Similar “binaural unmasking” can also be achieved for other types of stimuli, including speech, if they are presented in opposite phase to either ear. The improvement in speech intelligibility under these circumstances is called binaural intelligibility level difference (BILD). Nahum et al. (2008) therefore used BILD to test the theory.

In the “baseline” condition of their experiment, Nahum et al. (2008) measured the discrimination thresholds separately for the case in which words were identical in the two ears (and therefore there were no binaural disparity cues), and separately for the case in which words were phase-inverted in one ear (and therefore had the binaural disparity cues that facilitate detection in noise). The observed thresholds matched the predictions of ideal observer theory.

The second, crucial part of the experiment introduced manipulations in aspects of the task that should be irrelevant from the point of view of ideal observer predictions, but that nevertheless significantly affected detection thresholds. For example, in one test condition, trials in which the words were identical in the two ears were presented intermixed among trials in which the words were phase-inverted in one ear. This is called “interleaved tracks” in the psychoacoustical literature. As far as statistical detection theory is concerned, whether phase-identical and phase-inverted trials are presented in separate blocks or in interleaved tracks is irrelevant—the theory predicts optimal performance either way. The results, however, showed a clear difference—the presence of binaural disparities helped subjects much less in the interleaved tracks than in the baseline condition, especially when the two words to be distinguished differed only slightly (by a single phoneme). This is exactly what RHT would predict. Presumably, the backward search failed to find the optimally informative lower-level representation because this representation changed from one trial to the next. Consequently, the optimal task-related representation of the sounds, which is presumably provided by the activity of the disparity-sensitive neurons, perhaps in the MSO or the IC, cannot be efficiently accessed, and performance becomes suboptimal.

What are the implications of this for auditory scene analysis in masking experiments? RHT suggests that optimal performance can be achieved only if the conditions in which the experiments are run allow a successful search for the optimal neural representations. In this way, it puts in evidence the multiple representation levels of sounds in the auditory system.

One way of conceptualizing what is going on is therefore to think of auditory scene analysis as operating at a high-level representation, using evidence based on neural activity at lower representation levels. Thus, the auditory scene consists of separate tone and noise objects, because it presumably reflects the evidence supplied by the peripheral auditory system: the higher energy in the peripheral band centered on tone frequency.

Both low- and high-level representations have been studied electrophysiologically in the context of another masking paradigm, comodulation masking release (CMR). In CMR experiments, as in BILD, two masking conditions are contrasted. The first condition is a simple masking task with a noise masker and a pure tone target. As we already remarked, in this situation ideal observers, as well as well-trained humans, monitor the extra energy in the peripheral band centered on the target tone. In the second masking condition, the masker is “amplitude modulated,” that is, it is multiplied by an envelope that fluctuates at a slow rate (10–20 Hz). These fluctuations in the amplitude of the masker produce a “release from masking,” meaning that detecting the target tone becomes easier, so that tone detection thresholds drop. It is substantially easier for humans to hear a constant tone embedded in a fluctuating noise than one embedded in a noise of constant amplitude (Sound Example "Comodulation Masking Release" on the book's Web site <flag>).

The curious thing about CMR is that this drop in threshold is, in a sense, “too large” and depends on the bandwidth of the noise (figure 6.1). As we discussed earlier, there is an effective bandwidth, the critical band, around each tone frequency within which the noise is effective in masking the tone. In regular masking experiments, adding noise energy outside the critical band has no effect on the masking. It does not matter whether the noise energy increases if that increase is outside the critical band because the auditory nerve fibers centered on the target tone frequency “do not hear” and are not confused by the extra noise. In contrast, when the masker is amplitude modulated, adding extra noise energy with the same amplitude modulation outside the critical band does affect thresholds in a paradoxical way—more noise makes the tone easier to hear. It is the effect of masker energy away from the frequency of the target tone that makes CMR interesting to both psychoacousticians and electrophysiologists, because it demonstrates that there is more to the detection of acoustic signals in noise than filtering by auditory nerve fibers.

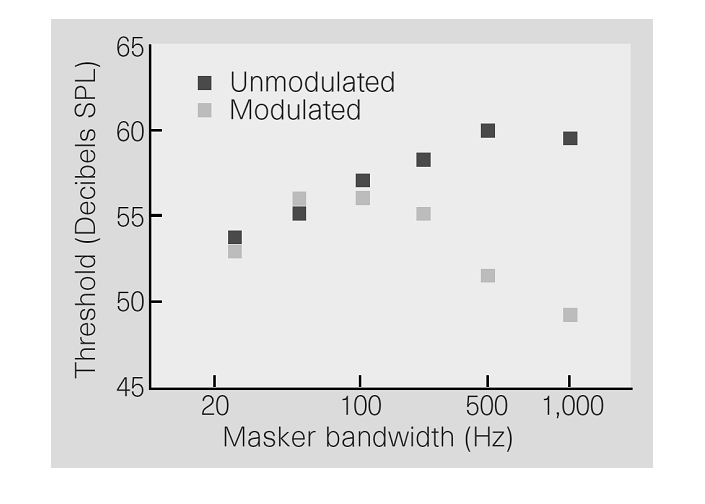
Figure 6.1

The lowest level at which a tone is detected as a function of the bandwidth of the noiseband that serves as the masker, for modulated and unmodulated noise. Whereas for unmodulated noise thresholds increase with increases in bandwidth (which causes an increase in the overall energy of the masker), wide enough modulated maskers are actually less efficient in masking the tone (so that tones can be detected at lower levels). This effect is called comodulation masking release (CMR).

Adapted from Moore (1999).

CMR has neurophysiological correlates as early as in the cochlear nucleus. Neurons in the cochlear nucleus often follow the fluctuations of the envelope of the masker, but interestingly, many neurons reduce their responses when masking energy is added away from the best frequency, provided the amplitude fluctuations of this extra acoustic energy follow the same rhythm. In figure 6.2, two masker conditions are contrasted: one in which the masker is an amplitude-modulated tone (left), and the other in which additional off-frequency amplitude-modulated tones are added to it, sharing the same modulation pattern as the on-frequency masker (right). The response to the masker is reduced by the addition of comodulated sidebands (compare the responses at the bottom row, left and right panels). This makes the responses to tones more salient in the comodulated condition.

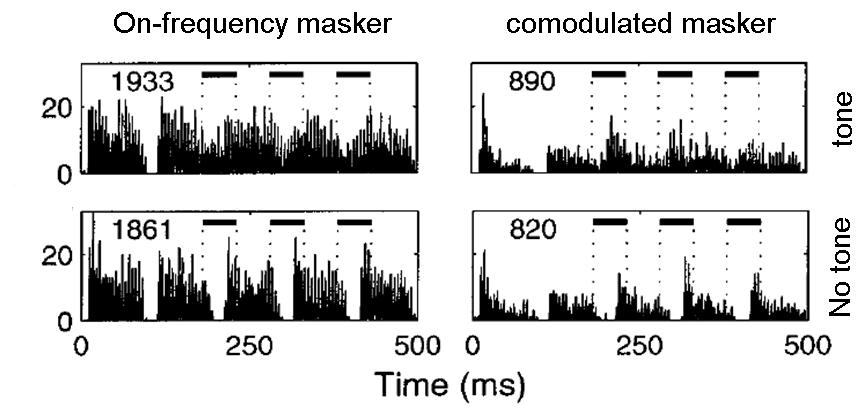
Figure 6.2

Responses of neurons in the cochlear nucleus to narrowband and wideband modulated maskers (left and right columns) with and without an added signal (top and bottom rows; here, the signal consisted of three tone pips in the valleys of the masker). In the comodulated condition, when the masker had larger bandwidth, the neural responses it evoked were reduced (compare the bottom panels, left and right). As a result, adding the tone to the wideband masker results in more salient responses. (Compare the top panels, left and right; tone presentations are marked by the bars at the top of each panel.)

Adapted from figure 3 in Pressnitzer et al. (2001).

What causes this reduction in the responses to the masker when flanking bands are added? Presumably, the underlying mechanism relies on the activity of “wideband inhibitor” neurons whose activity is facilitated by increasing the bandwidth of stimuli, which in turn inhibits other neurons in the cochlear nucleus. Nelken and Young (1994) suggested the concept of wideband inhibitors to account for the complex response properties of neurons in the dorsal cochlear nucleus, and possible candidates have been identified by Winter and Palmer (1995). A model based on observing the responses of single neurons in the cochlear nucleus, using the concept of the wideband inhibitor, indeed shows CMR (Neuert, Verhey, & Winter, 2004; Pressnitzer et al., 2001).

Thus, just like a human listener, an ideal observer, observing the responses of cochlear nucleus neurons, could detect a target tone against the background of a fluctuating masker more easily if the bandwidth of the masker increases. This picture corresponds pretty much to the low-level view of tone detection in noise.

Similar experiments have been performed using intracellular recordings from auditory cortex neurons (Las et al., 2005), so that changes of the neurons’ membrane potential in response to the sound stimuli could be observed. As in the cochlear nucleus, a fluctuating masker evokes responses that follow the envelope of the masker (figure 6.3, bottom, thick black trace). The weak tone was selected so that it did not evoke much activity by itself (figure 6.3, bottom, thin black trace). When the two were added together, the locking of the membrane potential to the envelope of the noise was abolished to a large extent (figure 6.3, bottom, thick gray trace). The responses to a weak tone in fluctuating noise can be compared to the responses to a strong tone presented by itself; these responses tend to be similar (figure 6.3), especially after the first noise burst following tone onset.

The CMR effect seen in these data is very pronounced—whereas in the cochlear nucleus, the manipulations of masker and target cause a quantitative change in the neuronal responses (some suppression of the responses to the noise as the bandwidth of the masker is widened; some increase in the responses to the target tone), the effects in cortex are qualitative: The pattern of changes in membrane potential stops signaling the presence of a fluctuating noise, and instead is consistent with the presence of a continuous tone alone.

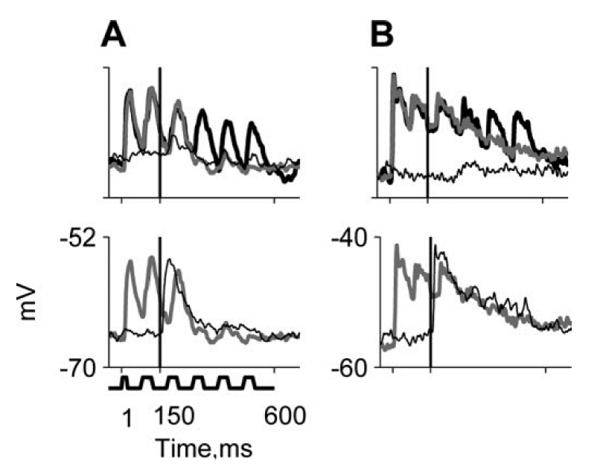
Figure 6.3

The top panels depict the responses of two neurons (A and B) to noise alone (thick black line; the modulation pattern is schematically indicated at the bottom of the figure), to a noise plus tone combination at the minimal tone level tested (gray line; tone onset is marked by the vertical line), and to a tone at the same tone level when presented alone (thin black line). The neurons responded to the noise with envelope locking—their membrane potential followed the on-off pattern of the noise. Adding a low-level tone, which by itself did not evoke much response, suppressed this locking substantially. The bottom panels depict the responses to a tone plus noise at the minimal tone level tested (gray, same as in top panel) and the response to a suprathreshold level that saturated the tone response (thin black line). The responses to a low-level tone in noise and to a high-level tone in silence follow a similar temporal pattern, at least after the first noise cycle following tone onset.

From figure 6 in Las, Stern, and Nelken (2005).

Originally, the suppression of envelope locking by low-level tones was suggested as the origin of CMR (Nelken, Rotman, & Bar Yosef, 1999). However, this cannot be the case—if subcortical responses are identical with and without a tone, then the cortex cannot “see” the tone either. It is a simple matter of neuroanatomy that, for the tone to affect cortical responses, it must first affect subcortical responses. As we discussed previously, correlates of CMR at the single-neuron level are already in the cochlear nucleus. Las et al. (2005) suggested, instead, that neurons like those whose activity is presented in figure 6.3 encode the tone as separate from the noise—as a separate auditory object. Presumably, once it has been detected, the tone is fully represented at the level of auditory cortex in a way that is categorically different from the representation of the noise.

These experiments offer a glimpse of the way low-level and high-level representations may operate. At subcortical levels, responses reflect the physical structure of the sound waveform, and therefore small changes in the stimulus (e.g., increasing the level of a tone from below to above its masked threshold) would cause a small (but measureable) change in firing patterns. At higher levels of the auditory system (here, in primary auditory cortex), the same small change may result in a disproportionally large change in activity, because it would signal the detection of the onset of a new auditory object. Sometimes, small quantitative changes in responses can be interpreted as categorical changes in the composition of the auditory scene, and the responses of the neurons in the higher representation levels may encode the results of such an analysis, rather than merely reflect the physical structure of the sound spectrum at the eardrum.

6.3 Simultaneous Segregation and Grouping

After this detailed introduction to the different levels of representation, let us return to the basics, and specify in more details what we mean by “elements of sounds” for the purpose of simultaneous grouping and segregation. After all, the tympanic membrane is put in motion by the pressure variations that are the sum of everything that produces sound in the environment. To understand the problem that this superposition of sounds poses, consider that the process that generates the acoustic mixture is crucially different from the process that generates a visual mixture of objects. In vision, things that are in front occlude those that are behind them. This means that occluded background objects are only partly visible and need to be “completed”; that is, their hidden bits must be inferred, but the visual images of objects rarely mix. In contrast, the additive mixing of sound waves is much more akin to the superposition of transparent layers. Analyzing such scenes brings its own special challenges.

Computationally, the problem of finding a decomposition of a sound waveform into the sum of waveforms emitted by multiple sources is ill-posed. From the perspective of the auditory brain, only the sound waveforms received at each ear are known, and these must be reconstructed as the sum of unknown waveforms emitted by an unknown number of sound sources. Mathematically, this is akin to trying to solve equations where we have only two knowns (the vibration of each eardrum) to determine an a priori unknown, and possibly quite large, number of unknowns (the vibrations of each sound source). There is no exact solution for such a problem. The problem of auditory scene analysis can be tackled only with the help of additional assumptions about the likely properties of sounds emitted by sound sources in the real world.

It is customary to start the consideration of this problem at the level of the auditory nerve representation (chapter 2). This is a representation of sounds in terms of the variation of energy in the peripheral, narrow frequency bands. We expect that the frequency components coming from the same source would have common features—for example, the components of a periodic sound have a harmonic relationship, and all frequency components belonging to the same sound source should start at the same time and possibly end at the same time; frequency components belonging to the same sound source might grow and decline in level together; and so on and so forth. If you still recall our description of modes of vibration and impulse responses from chapter 1, you may appreciate why it is reasonable to expect that the different frequency components of a natural sound might be linked in these ways in time and frequency. We will encounter other, possibly more subtle, grouping cues of this kind later.

The rules that specify how to select bits of sound that most likely belong together are often referred to as gestalt rules, in recognition of the importance of gestalt psychology in framing the issues governing perception of complex shapes. Thus, common onsets and common amplitude variations are akin to the common fate grouping principle in vision, according to which elements that move together in space would be perceived as parts of a single object. The so-called gestalt rules should be seen as heuristics that work reasonably well in most cases, and therefore may have been implemented as neural mechanisms.

Let us take a closer look at three of these grouping cues: common onset, harmonic structure, and common interaural time difference (ITDs), the latter being, as you may recall from chapter 5, a cue to the azimuth of a sound source. Whereas the first two turn out to be rather strong grouping cues, ITDs seem to have a somewhat different role.

6.3.1 Common Onsets

If several frequency components start at the same time, we are much more likely to perceive them as belonging to the same auditory object. This can be demonstrated in a number of ways. We will discuss one such experiment in details here; since it used common onsets for a number of purposes, it illustrates the level of sophistication of experiments dealing with auditory scene analysis. It is also interesting because it pits a high-level and a low-level interpretation of the results against each other.

Darwin and Sutherland (1984) used the fine distinction between the vowels /I/ and /e/ in English as a tool for studying the role of common onsets in auditory perception. These vowels differ slightly in the frequency of their rather low-frequency first formant (figure 6.4A and Sound Example "Onsets and Vowels Identity" on the book's Web site <flag>; see also chapter 4 for background on the structure of vowels). It is possible to measure a formant boundary—a first formant frequency below which the vowel would generally be categorized as /I/ and above it as /e/. Since the boundary is somewhat below 500 Hz, Darwin used a sound whose fundamental frequency is 125 Hz so that the boundary lies between the third and the fourth harmonics (figure 6.4A). The perceived frequency of the first formant depends on the relative levels of the third and fourth harmonics. Figure 6.4A illustrates three cases: When the third harmonic is substantially louder than the fourth harmonic, the formant frequency is definitely 375 Hz, and an /I/ is perceived. In the opposite case, when the fourth harmonic is substantially louder than the third harmonic, the formant frequency is definitely 500 Hz and an /e/ is perceived. When both harmonics have about the same level, the perceived first formant frequency is between the two. This sound has an ambiguous quality, and listeners perceived it as an /I/ or as an /e/ with similar probabilities (Sound Example "Onsets and Vowels Identity" <flag>). 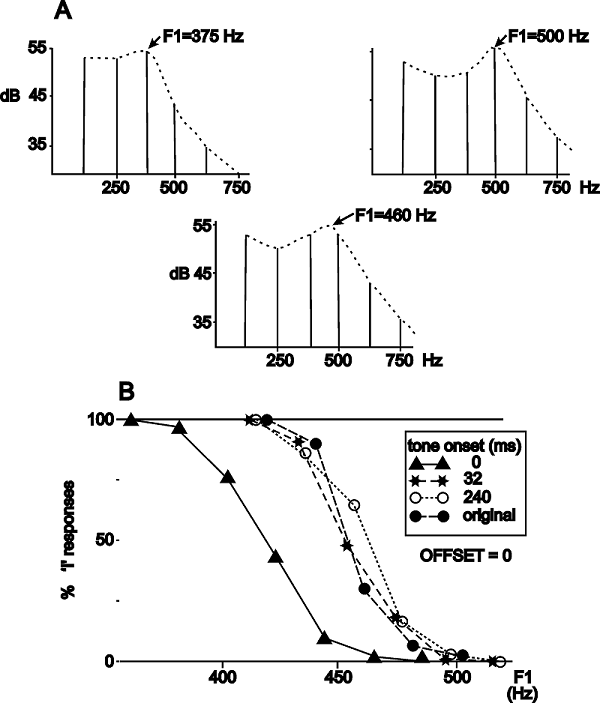In general, vowel identity judgments for such sounds depended on this nominal first formant frequency, as expected, and there was a reasonably sharp transition between judgments of /I/ and /e/ as this first formant frequency increased from 375 to 500 Hz (figure 6.4B, full dots). Darwin and Sutherland called this first formant frequency value “the nominal first formant frequency.”

Figure 6.4

(A) Illustration of the principle of the experiment. The two top spectra illustrate the first-formant region of the vowels /I/ and /e/ used in the experiment. The difference between them is in first formant frequency (375 Hz for /I/, 500 Hz for /e/). At a pitch of 125 Hz, these fall exactly on the third (left) and fourth (right) harmonics of the fundamental, which are therefore more intense than their neighbors. When the levels of the two harmonics are approximately equal, as in the middle spectrum, the first formant frequency is perceived between the two harmonics (here, at the category boundary between /I/ and /e/). Thus, by manipulating the relative levels of these two harmonics, it is possible to pull the perceived vowel between the extremes of /I/ and /e/. (B) Perceptual judgments for the identity of the vowel (filled circles), for the vowel with its fourth harmonic increased in level (triangles), and for the vowel with the fourth harmonic increased in level and starting before the rest of the vowel (stars and open circles). Onset asynchrony abolished the effect of the increase in level.

From figures 1 and 3 in Darwin and Sutherland (1984).

Darwin and Sutherland then introduced a slight modification of these stimuli. In order to shift the first formant, they increased the level the fourth harmonic, 500 Hz, of the standard vowel by a fixed amount. By doing so, the first formant frequency that is actually perceived is pulled toward higher values, so the sound should be judged as /e/ more than as /I/. The effect is reasonably large, shifting the boundary by about 50 Hz (figure 6.4B, triangles; Sound Example "Onsets and Vowels Identity" <flag>).

The heart of the experiment is a manipulation whose goal is to reverse this effect. Darwin and Sutherland’s idea was to reduce the effect of the increase in the level of the fourth harmonic by supplying hints that it is not really part of the vowel. To do that, they changed its onset and offset times, starting it before or ending it after all the other harmonics composing the vowel. Thus, when the fourth harmonic started 240 ms earlier than the rest, subjects essentially disregarded its high level when they judged the identity of the vowel (figure 6.4B, circles and stars; Sound Example "Onsets and Vowels Identity" <flag>). A similar, although smaller, perceptual effect occurred with offsets.

These results lend themselves very naturally to an interpretation in terms of scene analysis: Somewhere in the brain, the times and levels of the harmonics are registered. Note that these harmonics are resolved (chapters 2 and 3), as they are far enough from each other to excite different auditory nerve fibers. Thus, each harmonic excites a different set of auditory nerve fibers, and a process that uses common onset as a heuristic observes this neural representation of the spectrotemporal pattern. Since the fourth harmonic started earlier than the rest of the vowel, this process segregates the sounds into two components: a pure tone at the frequency of the fourth harmonic, and the vowel. As a result, the energy at 500 Hz has to be divided between the pure tone and the vowel. Only a part of it is attributed to fourth harmonic of the vowel, and the vowel is therefore perceived as more /I/-like, causing the reversal of the shift in the vowel boundary.

However, there is another possible interpretation of the same result. When the 500-Hz tone starts before the other harmonics, the neurons responding to it (the auditory nerve fibers as well as the majority of higher-order neurons throughout the auditory system) would be activated before those responding to other frequencies, and would have experienced spike rate adaptation. Consequently, their firing rates would have declined by the time the vowel started and the other harmonics came in. At the moment of vowel onset, the pattern of activity across frequency would therefore be consistent with a lower-level fourth harmonic, pulling the perception back toward /I/. We have here a situation similar to that discussed earlier in the context of masking—both high-level accounts in terms of scene analysis or low-level accounts in terms of subcortical neural firing patterns can be put forward to explain the results. Is it possible to falsify the low-level account?

Darwin and Sutherland (1984) tried to do this by adding yet another element to the game. They reasoned that, if the effect of onset asynchrony is due to perceptual grouping and segregation, they should be able to reduce the effect of an asynchronous onset by “capturing” it into yet another group, and they could then try to signal to the auditory system that this third group actually ends before the beginning of the vowel. They did this by using another grouping cue: harmonicity. Thus, they added a “captor tone” at 1,000 Hz, which started together with the 500 Hz tone before vowel onset, and ended just at vowel onset. They reasoned that the 500 Hz and the 1,000 Hz would be grouped by virtue of their common onset and their harmonic relationship. Ending the 1,000 Hz at vowel onset would then imply that this composite object, that is, both the 1,000- and the 500-Hz component, disappeared from the scene. Any 500-Hz sound energy remaining should then be attributed to, and grouped perceptually with, the vowel that started at the same time that the captor ended, and the 500-Hz component should exert its full influence on the vowel identity. Indeed, the captor tone reversed, at least to some degree, the effect of onset asynchrony (Sound Example "Onsets and Vowels Identity" <flag>). This indicates that more must be going on than merely spike rate adaptation at the level of the auditory nerve, since the presence or absence of the 1,000-Hz captor tone has no effect on the adaptation of 500-Hz nerve fibers.

The story doesn’t end here, however, since we know today substantially more than in 1984 about the sophisticated processing that occurs in early stages of the auditory system. For example, we already encountered the wideband inhibition in the cochlear nucleus in our discussion of CMR. Wideband inhibitor neurons respond poorly to pure tones, but they are strongly facilitated by multiple tones, or sounds with a wide bandwidth. They are believed to send widespread inhibitory connections to most parts of the cochlear nucleus.

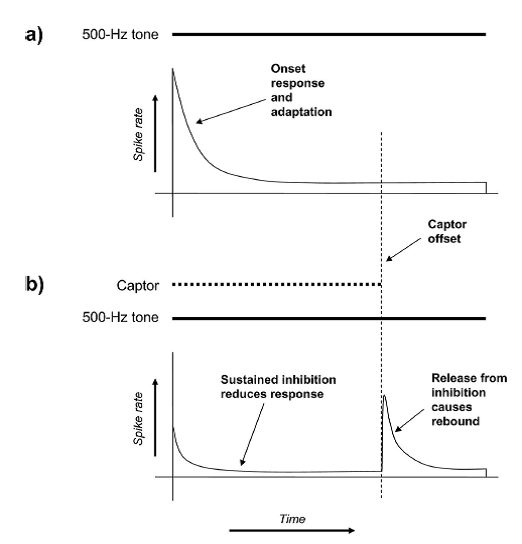
Figure 6.5

Illustration of the effect of wideband inhibition when a captor tone is used to remove the effects of onset asynchrony. (A) Responses to the fourth harmonic (at 500 Hz) consist of an onset burst followed by adaptation to a lower level of activity. (B) In the presence of the captor, wideband inhibition would reduce the responses to the 500-Hz tone. Furthermore, at the offset of the captor tone, neurons receiving wideband inhibition tend to respond with a rebound burst (as shown by Bleeck et al. 2008).

From figure 2 in Holmes and Roberts (2006).

Wideband inhibition could supply an alternative low-level account of the effects of the captor tone (figure 6.5). When the captor tone is played, it could (together with the 500-Hz tone) activate wideband inhibition, which in turn would reduce the responses of cochlear nucleus neurons responding to 500 Hz, which would consequently fire less but therefore also experience less spike rate adaptation. When the 1,000-Hz captor stops, the wideband inhibition ceases, and the 500-Hz neurons would generate a “rebound” burst of activity. Because the 1,000-Hz captor ends when the vowel starts, the rebound burst in the 500-Hz neurons would be synchronized with the onset bursts of the various neurons that respond to the harmonics of the vowel, and the fact that these harmonics, including the 500-Hz tone, all fired a burst together will make it look as if they had a common onset.

Thus, once again we see that it may be possible to account for a high-level “cognitive” phenomenon in terms of relatively low-level mechanisms. Support for such low-level accounts comes from recent experiments by Holmes and Roberts (2006; Roberts & Holmes, 2006, 2007). For example, wideband inhibition is believed to be insensitive to harmonic relationships, and indeed it turns out that captor tones don’t have to be harmonically related to the 500-Hz tone. They can even consist of narrow noisebands rather than pure tones. Almost any sound capable of engaging wideband inhibition will do. The captor tones can even be presented to the contralateral ear, perhaps because wideband inhibition can operate binaurally as well as monaurally. Furthermore, there are physiological results that are consistent with the role of the wideband inhibitor in this context: Bleeck et al. (2008) recorded single-neuron responses in the cochlear nucleus of guinea pigs, and demonstrated the presence of wideband inhibition, as well as the resulting rebound firing at captor offset, using harmonic complexes that were quite similar to those used in the human experiments.

But this does not mean that we can now give a complete account of these auditory grouping experiments in terms of low-level mechanisms. For example, Darwin and Sutherland (1984) already demonstrated that increasing the duration of the 500-Hz tone beyond vowel offset also changes the effect it has on the perceived vowel, and these offset effects cannot be accounted for either by adaptation or by wideband inhibition. Thus, there may be things left to do for high-level mechanisms. In this section, however, it has hopefully become clear that any such high-level mechanisms will operate on a representation that has changed from the output of the auditory nerve. For example, adaptation, wideband inhibition, and rebounds will emphasize onsets and offsets, and suppress responses to steady-state sounds. Each of the many processing stations of the auditory pathway could potentially contribute to auditory scene analysis (and, of course, all other auditory tasks). The information that reaches the high-level mechanisms reflects the activity in all of the preceding processing stations. For a complete understanding of auditory scene analysis, we would like to understand what each of these processing stations does and how they interconnect. This is obviously an enormous research task.

6.3.2 Fundamental Frequency and Harmonicity

We will illustrate the role of pitch and harmonicity in auditory scene analysis by using a familiar task—separating the voices of two simultaneous talkers. Here we discuss a highly simplified, yet perceptually very demanding version of this, namely, the identification of two simultaneously presented vowels.

In such a double-vowel experiment, two vowels are selected at random from five or six possible vowels (e.g., /a/, /e/, /i/, /o/, /u/, or close language-adjusted versions). The two chosen vowels are then presented simultaneously, and the subject has to identify both (Sound Example "Double Vowels" on the book's Web site <flag>). The vowels would be easily discriminated if presented one after the other, but subjects make a lot of errors when asked to identify both when they are presented together. With five possible vowels, when subjects cannot make much headway by simply guessing, their performance would be only around 4% correct identification for both vowels. When both vowels have the same pitch, identification levels are in fact substantially above chance (figure 6.6): Depending on the experiment, correct identification rates may be well above 50%. Still, although well above chance, this level of performance means that, on average, at least one member of a pair is misidentified on every other stimulus presentation—identifying double vowels is a hard task.

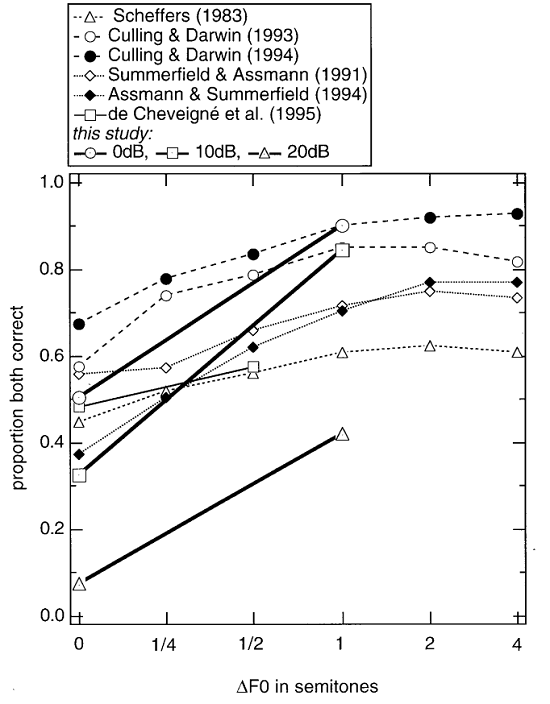
Figure 6.6

Summary of a number of studies of double vowel identification. The abscissa represents the difference between the fundamental frequencies of the two vowels. The ordinate represents the fraction of trials in which both vowels were identified correctly. The data from de Cheveigné et al. (1997a) represents experiments in which the two vowels had different sound levels (as indicated in the legend). The difference in fundamental frequency was as useful, or even more useful, for the identification of vowels with different sound levels, a result that is inconsistent with pure-channel selection and may require harmonic cancellation, as discussed in the main text.

From figure 1 of de Cheveigné et al. (1997).

The main manipulation we are interested in here is the introduction of a difference in the fundamental frequency (F0) of the two vowels. When the two vowels have different F0s, correct identification rates increase (figure 6.6), at least for F0 differences of up to 1/2 semitone (about 3%). For larger differences in F0, performance saturates. Thus, vowels with different F0s are easier to discriminate than vowels with the same F0.

What accounts for this improved performance? There are numerous ways in which pitch differences can help vowel segregation. For example, since the energy of each vowel is not distributed equally across frequency, we would expect the responses of some auditory nerve fibers to be dominated by one vowel and those of other fibers to be dominated by the other vowel. But since the activity of auditory nerve fibers in response to a periodic sound is periodic (see chapter 3), those fibers whose activity is dominated by one vowel should all fire with a common underlying rhythm, because they all phase lock to the fundamental frequency of that vowel. If the vowels differ in F0, then each vowel will impose a different underlying rhythm on the population of nerve fibers it activates most strongly. Thus, checking the periodicity of the responses of each auditory nerve fiber should make it possible to assign different fibers to different vowels, and in this way to separate out the superimposed vowel spectra. Each vowel will dominate the activity of those fibers whose best frequency is close to the vowel’s formant frequencies. Thus, the best frequencies of all the fibers that phase lock to the same underlying periodicity should correspond to the formant frequencies of the vowel with the corresponding F0. This scheme is called “channel selection”.

The plausibility of channel selection has indeed been demonstrated with neural activity in the cochlear nucleus (Keilson et al. 1997). This study looked at responses of “chopper” neurons in the cochlear nucleus to vowel sounds. Chopper neurons are known to phase lock well to the F0 of a vowel. In this study, two different vowels were used, one /I/, and one /ae/, and these were embedded within the syllables /bIs/ or /baes/. The /I/ had a F0 of 88 Hz, the /ae/ a slightly higher F0 of 112 Hz. During the experiment, the formants of the /I/ or the /ae/ sounds were tweaked to bring them close to the best frequency (BF) of the recorded chopper neuron. Figure 6.7A shows the response of the neuron to the /I/ whose second formant frequency was just above the neuron’s BF. The left column shows the instantaneous firing rate of the neuron during the presentation of the syllable. The horizontal line above the firing rate histogram shows when the vowel occurred. Throughout the stimulus, the neuron appears to fire with regular bursts of action potentials, as can be seen from the peaks in the firing rate histogram. The right column shows the frequency decomposition of the firing rate during the vowel presentation. The sequence of peaks at 88 Hz and its multiples demonstrate that the neuron indeed emitted a burst of action potentials once every period of the vowel. Figure 6.7D (the bottom row), in comparison, shows the responses of the same neuron to the /ae/ sound with the slightly higher F0. Again, we see the neuron responds with regular bursts of action potentials, which are synchronized this time to the stimulus F0 of 112 Hz (right dot).

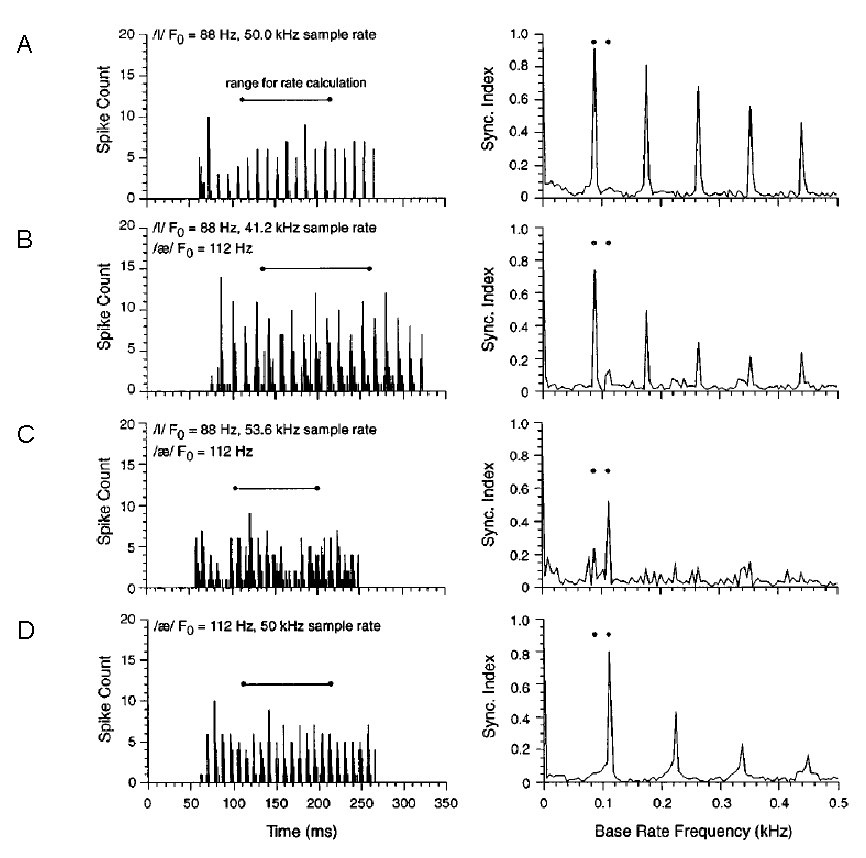
Figure 6.7

(A and D) Responses of a chopper neuron to the syllables /bIs/ and /baes/ with F0 or 88 or 112 Hz, respectively. (B and C) Responses of the same neuron to mixtures of /bIs/ and /baes/ presented at the same time. The plots on the left show poststimulus time histograms (PSTHs) of neural discharges, representing the instantaneous firing rate of the neuron during stimulus presentation. The lines above the PSTHs indicate when the vowels /I/ and /ae/ occurred during the syllables. The plots on the right are the frequency decompositions of the PSTHs during vowel presentation, measuring the locking to the fundamental frequency of the two vowels: A sequence of peaks at 88 Hz and its multiples indicate locking to the fundamental frequency of the /I/ sound, while a sequence of peaks at 112 Hz and its multiples indicate locking to the fundamental frequency of the /ae/ sound. The two fundamental frequencies are indicated by the dots above each panel.

From figure 3 of Keilson et al. (1997).

The two middle rows, figures 6.7B and C, show responses of the same neuron to “double vowels,” that is, different mixtures of /I/ and /ae/. The firing patterns evoked by the mixed stimuli are more complex; However, the plots on the right clearly show that the neuron phase locks either to the F0 of the /I/ of 88 Hz (figure 6.7B) or to the F0 of the /ae/ of 112 Hz (figure 6.7C), but not to both. Which F0 “wins” depends on which of the stimuli has more energy at the neuron’s BF.

The temporal discharge patterns required to make channel selection work are clearly well developed in the cochlear nucleus. But is this the only way of using periodicity? A substantial amount of research has been done on this question, which cannot be fully reviewed here. We will discuss only a single thread of this work—the somewhat unintuitive idea that pitch is used to improve discrimination is by allowing harmonic cancellation (de Cheveigné, 1997; de Cheveigné et al., 1995, 1997a, 1997b). Effectively, the idea is that the periodicity of one vowel could be used to remove it from a signal mixture, and the remainder could then be examined to identify further vowels or other background sounds. One very simple circuit that implements such a scheme is shown in figure 6.8A.

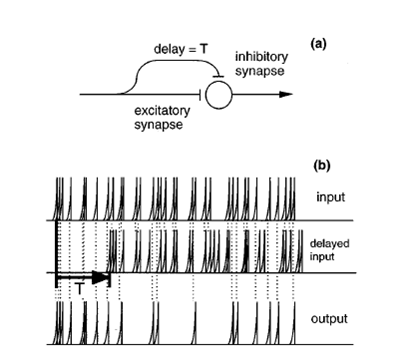
Figure 6.8

A cancellation filter. (A) The neural architecture. The same input is fed to the neuron through an excitatory synapse and through an inhibitory synapse, with a delay, T, between them. As a result, any spike that appears exactly T seconds following another spike is deleted from the output spike train. (B) An example of the operation of the cancellation filter. Only spikes that are not preceded by another spike T seconds earlier appear in the output.

From figure 1 of de Cheveigné (1997a).

The inhibitory delay line shown in figure 6.8A acts as a filter that deletes every spike that occurs at a delay T following another spike. If the filter is excited by a periodic spike train with a period T, the output rate would be substantially reduced. If the spike train contains two superimposed trains of spikes, one with a period of T and the other with a different period, the filter would remove most of the spikes that belong to the first train, while leaving most of the spikes belonging to the other. Suppose now that two vowels are simultaneously presented to a subject. At the output of the auditory nerve, we position two cancellation filters, one at a delay corresponding to the period of one vowel, the other at the period of the other vowel. Finally, the output of each filter is simply quantified by its rate—the rate of the leftover spikes, after canceling those that presumably were evoked by the other vowel.

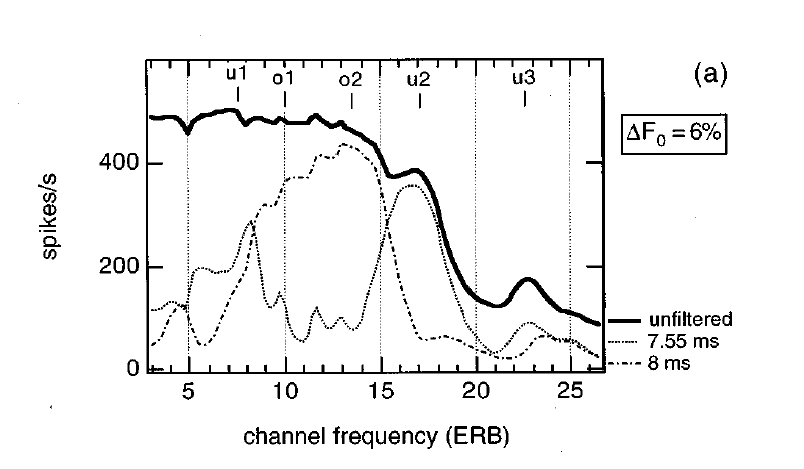
Figure 6.9

A simulation of cancellation filters. The thick black line represents the overall firing rate of auditory nerve fibers stimulated by a double vowel consisting of /o/ and /u/ played simultaneously. The thin lines represent the output of cancellation filters, one at the pitch of each of the two vowels, positioned at the output of each auditory nerve fiber. The representation of the formants is recovered at the output of the cancellation filters.

From figure 3a of Cheveigné et al. (1997a).

The results of such a process is illustrated in figure 6.9, which is derived from a simulation. The two vowels in this example are /o/ and /u/. The vowel /o/ has a rather high first formant and a rather low second formant (marked by o1 and o2 in figure 6.9), while /u/ has a lower first formant and a higher second formant (marked by u1 and u2). The thick line represents the rate of firing of the auditory nerve fiber array in response to the mixture of /o/ and /u/. Clearly, neither the formants of /o/ nor those of /u/ are clearly represented. The dashed lines are the rates at the output of two cancellation filters, tuned to the period of each of the two vowels. The vowel /u/ had an F0 of 125 Hz, with a period of 8 ms; /o/ had an F0 of 132 Hz, with a period of about 7.55 ms. Thus, the cancellation filter with a period of 8 ms is expected to cancel the contribution of /u/ to the firing rate, and indeed the leftover rate shows a broad peak where the two formants of /o/ lie. Conversely, the cancellation filter with a period of 7.55 ms is expected to cancel the contribution of /o/ to the firing rate, and indeed the leftover rate has two peaks at the locations of the formant frequencies of /u/. So the cancellation scheme may actually work.

Now we have two mechanisms that may contribute to double-vowel identification: channel selection and periodicity cancellation. Do we need both? De Cheveigné and his colleagues investigated the need for periodicity cancellation in a number of experiments. One of them consisted of testing the discriminability, not just of periodic vowels, but also of nonperiodic vowels (de Cheveigné et al., 1995; De Cheveigné et al., 1997b). The latter were produced by shifting their harmonics a bit. This creates an aperiodic sound that has a poorly defined pitch, but nevertheless a clear vowel identity (Sound Example "Inharmonic Vowels" on the book's Web site <flag>). When periodic and aperiodic vowels are presented together, only the periodic vowels can be canceled with the scheme proposed in figure 6.8, but the aperiodic vowel should nevertheless be clearly represented in the “remainder.” Indeed, aperiodic vowels could be more easily discriminated in double-vowel experiments with mixtures of periodic and aperiodic vowels. That result can be easily explained with the cancellation idea, but is harder to explain in terms of channel selection. The channels dominated by the aperiodic vowels would presumably lack the “tagging” by periodicity, and therefore nothing would link these channels together. Thus, channel selection alone cannot explain how inharmonic vowels can be extracted from a mixture of sounds.

Another line of evidence that supports the cancellation theory comes from experiments that introduce sound intensity differences between the vowels. A rather quiet vowel should eventually fail to dominate any channel, and the channel selection model would therefore predict that differences of F0 would be less useful for the weaker vowel in a pair. Harmonic cancellation predicts almost the opposite: It is easier to estimate the F0 of the higher-level vowel and hence to cancel it in the presence of F0 differences. Consequently, the identification of the weak vowel should benefit more from the introduction of F0 differences. Indeed, de Cheveigné and colleagues (1997a) demonstrated that the introduction of differences in F0 produced a greater benefit for identifying the weaker than the louder vowel in a pair (see figure 6.6 for some data from that experiment). Thus, the overall pattern of double-vowel experiments seems to support the use of harmonic cancellation.

But is there any physiological evidence for harmonic cancellation operating in any station of the auditory pathway? In the cochlear nucleus, we have seen that chopper neurons tend to be dominated by the periodicity of the vowel that acoustically dominates their input. Other kinds of neurons seem to code the physical complexity of the mixture stimulus better, in that their responses carry evidence for the periodicity of both vowels. However, there is no evidence for cochlear nucleus neurons that would respond preferentially to the weaker vowel in a pair, as might be expected from cancellation. The same is true in the inferior colliculus (IC), as was shown by Sinex and colleagues (Sinex & Li, 2007). Neurons in the central nucleus of the IC are sensitive to the composition of the sound within a narrow frequency band around their best frequency; when this band contains harmonics of both vowels, their activity would reflect both periodicities. Although IC neurons have not been tested with the same double-vowel stimuli used by Keilson et al. (1997) in the cochlear nucleus (figure 6.7), the available data nevertheless indicates that responses of the neurons in inferior colliculus would follow pretty much the same rules as those followed by cochlear nucleus neurons. Thus, we would not expect IC neurons to show cancellation of one vowel or the other. Other stations of the auditory pathways have not been tested with similar stimuli. Admittedly, none of these experiments is a critical test of the cancellation filter. For example, cancellation neurons should have “notch” responses to periodicity—they should respond to sounds of all periodicities except around the period they preferentially cancel. None of the above experiments really tested this prediction.

What are we to make of all this? Clearly, two simultaneous sounds with different F0s are easier to separate than two sounds with the same F0. Thus, periodicity is an important participant in auditory scene analysis. Furthermore, electrophysiological data from the auditory nerve, cochlear nucleus, and the IC indicate that, at least at the level of these stations, it may be possible to improve vowel identification through channel selection by using the periodicity of neural responses as a tag for the corresponding channels. On the other hand, psychoacoustic results available to date seem to require the notion of harmonic cancellation—once you know the periodicity of one sound, you “peel” it away and study what’s left. However, there is still no good electrophysiological evidence for harmonic cancellation.

To a large degree, therefore, our electrophysiological understanding lags behind the psychophysical results. The responses we see encode the physical structure of the double-vowel stimulus, rather than the individual vowels; they do so in ways that may help disentangle the two vowels, but we don’t know where and how that process ends.

Finally, none of these models offers any insight into how the spectral profiles of the two vowels are interpreted and recognized (de Cheveigné & Kawahara, 1999). That stage belongs to the phonetic processing we discussed in chapter 4, but it is worth noting here that the recovered spectra from double-vowel experiments would certainly be distorted, and could therefore pose special challenges to any speech analysis mechanisms.

6.3.3 Common Interaural Time Differences

Interaural time differences (ITDs) are a major cue for determining the azimuth of a sound source, as we had seen in chapter 5. When a sound source contains multiple frequency components, in principle all of these components share the same ITD, and therefore common ITD should be a good grouping cue. However, in contrast with common onsets and harmonicity, which are indeed strong grouping cues, common ITD appears not to be.

This is perhaps surprising, particularly since some experiments do seem to indicate a clear role for ITD in grouping sounds. For example, Darwin and Hukin (1999) simultaneously presented two sentences to their participants. The first sentence was an instruction of the type “Could you please write the word bird down now,” and the second was a distractor like “You will also hear the sound dog this time.” The sentences were arranged such that the words “bird” and “dog” occurred at the same time and had the same duration (Sound Example "ITD in the Perception of Speech" on the book's Web site <flag>). This created confusion as to which word (bird or dog) was the target, and which the distractor. The confusion was measured by asking listeners which word occurred in the target sentence (by pressing b for “bird” or d for “dog” on a computer keyboard), and scoring how often they got it wrong. Darwin and Hukin then used two cues, F0 and ITD, to reduce this confusion. They found that, while rather large F0 differences reduced the confusion by only a small (although significant) amount, even small ITDs (45 μs left ear–leading for one sentence, 45 μs right ear–leading for the other one) reduced the confusion by substantially larger amounts. Furthermore, Darwin and Hukin pitted F0 and ITD against each other, by presenting the sentences, except for the target word “dog,” with different F0s, and making the F0 of the target word the same as that of the distractor sentence. They then played these sentences with varying ITDs, and found that ITD was actually more powerful than F0 – in spite of the difference in F0 between the target word and the rest of the sentence, listeners were substantially more likely to associate the word with the rest of the sentence, presumably because both had the same ITD. This experiment suggests that ITD has a powerful role in linking sequential sounds—we tend to associate together elements of sounds that occur sequentially with the same ITD. However, this is a different situation from the one we have been discussing so far, where we studied cues for grouping acoustic components that overlap in time. So what is the role of ITD in simultaneous grouping?

The fact that ITD is only a weak cue for simultaneous grouping was reported initially by Culling and Summerfield (1995). We will describe here a related experiment that shows the same type of effects, using a phenomenon we described earlier when discussing the role of common onsets: the shifts in the category boundary between /I/ and /e/ due to the manipulation of one harmonic. We have already discussed the role of onset asynchrony in modifying the degree of fusion of a harmonic with the rest of the tone complex. Let us now consider a similar experiment by Darwin and Hukin (1999), which shows that ITDs exercise a much smaller influence on the perceptual fusion of frequency components than common onsets.

As in the study of onset asynchrony, Darwin and Hukin (1999) generated a set of vowels spanning the range between /I/ and /e/ by modifying the first formant. The vowels had a constant pitch of 150 Hz. Then, they extracted the 600-Hz (fourth) harmonic of the vowel, and presented the vowel without its fourth harmonic at one ITD, and the missing harmonic separately with either the same or a different ITD. Perhaps surprisingly, changing the ITD of this harmonic had no effect on whether the vowel was perceived as an /I/ and /e/, even though we might have expected that changing the ITD of the fourth harmonic would separate it from the rest of the vowel, and thereby change its formants. To further demonstrate the lack of effect of ITD on simultaneous grouping, Darwin and Hukin repeated a manipulation we already met—increasing the level of the fourth harmonic, which made more of the vowels sound like /e/, since this manipulation shifted the first formant peak to higher values. As before, they tried now to reduce the effect of the higher level of the fourth harmonic by changing its ITD (similarly to the attempt to reduce the effect of harmonic level by manipulating its onset). But the effects of increasing the level of the fourth harmonic were essentially the same, regardless of whether or not it had the same ITD as the rest of the vowel. ITD therefore seems not to operate as a simultaneous grouping cue, or at least it cannot ungroup simultaneous frequency components that have been grouped on the basis of common onset and harmonicity.

How do we understand the seemingly contradictory results of the two experiments? Darwin and Hukin suggested that the role of the sentence in the dog versus bird experiment was to direct the auditory system to process auditory objects from a specific location in space, leading to the strong effect of ITD, not because of its intrinsic properties, but because it suggested that the word occurred in the same spatial location. In the second experiment, there was no such cuing, and therefore other acoustic cues (e.g., harmonicity) overrode the effects of ITD.

6.3.4 Neural Correlates of Simultaneous Segregation and Grouping

Although this section has presented a number of neural correlates of segregation of simultaneous sounds and possible mechanisms that contribute to this goal, we did not mention many neural correlates of the actual endpoint of this process—the representation of the segregated sounds. The reason for this is simple: There are very few examples of this in the literature. One possible example is the case of CMR in auditory cortex, as described in the previous section. However, CMR is a somewhat artificial construct. We would really like to be able to show examples of mixtures of natural sounds being segregated and represented separately somewhere in the brain.

Some evidence that this may occur at the level of primary auditory cortex has been offered by Bar-Yosef and colleagues (Bar-Yosef & Nelken, 2007; Bar-Yosef, Rotman, & Nelken, 2002; Nelken & Bar-Yosef, 2008). They studied responses to bird songs extracted from natural recordings. Because these recordings were made “in the real world,” the songs were accompanied by additional acoustic components such as echoes and background noises. It is possible, however, to separate out the “foreground” bird song from the background noise, and to present separately the cleaned “foreground only” song or the much quieter remaining background sounds to neurons (Sound Example "Bird Songs and their Backgrounds" on the book's Web site <flag>). Figure 6.10 displays the responses of four cat auditory cortex neurons to these stimuli. The top panel shows the responses of these neurons to pure tones with different frequencies and levels. These “frequency response area” (FRA) plots reveal a typical V-shaped tuning curve with best frequencies around 4 kHz, close to the center frequency of the bird chirps that were used in these experiments. On top of the FRAs, the thick dark gray line represents the frequency content of the clean bird chirp. Below the FRAs, the different stimuli and the resulting responses are shown. The responses are displayed as rasters—there are twenty repeats of each sound and, in each repeat, a dot represents the time of occurrence of a spike. The stimuli are shown as spectrograms (described in chapter 1).

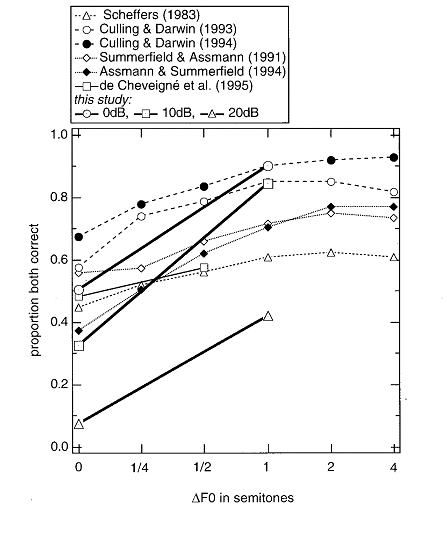
Figure 6.10

Responses of four neurons to natural bird chirps and their modifications. The top panels display in gray levels the responses of these neurons to tones of varying frequencies and levels (along the abscissa and ordinate, respectively), a representation called frequency response area (FRA). The bottom panels represent the responses of the neurons to three stimuli: the natural bird chirp (bottom), the clean main chirp (middle), and the leftover signal (top). In each case, the spectrogram is displayed below a raster plot, using dots to display the time of occurrence of spikes in twenty presentations of each of the stimuli. The thick dark gray lines on top of the FRAs represent the frequency content of the clean chirp ('Main').

From figure 13 of Bar-Yosef and Nelken (2007).

Three stimuli are shown for each neuron. The bottom stimulus is a segment from a natural recording, including the bird chirp and all the rest of the sound, which includes echoes (the ”halo” around the chirps) and rustling (apparent as a mostly uniform background at all frequencies). The middle stimulus is the “foreground only” bird chirp, and the upper stimulus is the remainder after removal of the chirp, that is, just the echoes and background. Considering that most of the sound energy of the original, natural sound is contained in the bird chirp, the responses to the original recording and the cleaned chirp (bottom and middle rows) can be surprisingly different. In fact, in the examples shown here, the responses to the background, played alone, were much more similar to the responses to the full natural stimulus than were the responses to the foreground only stimulus.

The responses of these neurons may be interpreted as correlates of the end point of a process of scene analysis—they respond to some, but not all, of the components of an auditory scene. In fact, they respond to the weaker components in the scene. Perhaps other neurons respond to the clean chirp rather than to the background, although Bar-Yosef and Nelken (2007) did not describe such neurons. Alternatively, it may be that these neurons are really doing the hard part of auditory scene analysis—the foreground bird chirp is easy to hear. Hearing the background is harder, but potentially very important: The sounds of prey or predators may lie hidden in the background! Surveillance of the subtler background sounds might be a key function of auditory cortex. In fact, the same group presented data suggesting that responses in IC to these sounds are usually more closely related to the physical structure of the sounds, and therefore more strongly influenced by the high-intensity foreground. Thalamic responses, on the other hand, would appear to be more similar to the cortical responses (Chechik et al., 2006). So far, however, there are only very few such examples in the literature. Much more experimental data with additional stimuli will be required to fully assess the role of cortex in auditory scene analysis.

6.4 Nonsimultaneous Grouping and Segregation: Streaming

Simultaneous grouping and segregation is only one part of auditory scene analysis. Sound sources are often active for a long time, and the way they change (or not) as a function of time has important consequences for the way they are perceived. We already encountered an effect of this kind—the effect of ITD on grouping, which was large for sequential sounds but weak for simultaneous grouping.

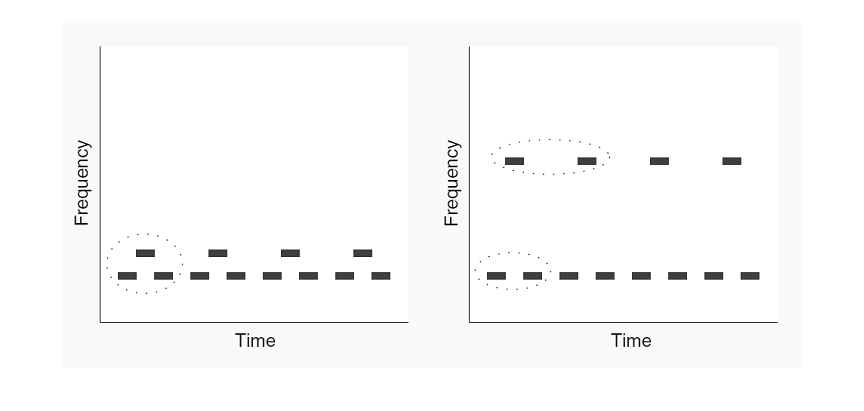
Figure 6.11

Streaming is the breakdown of a sequence of tones into two “streams.” In this illustration, tones of two frequencies are presented successively, with the higher tone at half the rate of the lower one. When the frequency separation between the two is small, the result is a single stream of sounds with a basic three-tone galloping melody. When the frequency separation between the two tones is large, the sequence breaks down into two streams, one composed of the low-frequency tones, the other of the high-frequency tones.

From figure 1 of Schnupp (2008)[DH1] .

A number of examples of this kind have been studied in the literature. Possibly the simplest form of streaming uses two pure tones (Sound Example "Streaming with Alternating Tones" on the book's Web site <flag>). The two tones are played alternately at a fixed rate. If the rate of presentation is slow and the interval between the two tones is small, the result is a simple melody consisting of two alternating tones. However, if the rate of presentation is fast enough and the frequency separation between the two tones is large enough, the melody breaks down into two streams, each consisting of tones of one frequency. A more interesting version of the same phenomenon, which has been studied intensively recently, is the “galloping,” or “ABA” rhythm paradigm. This paradigm, first introduced by van Noorden in his PhD thesis (Van Noorden, 1975), is illustrated in figure 6.11 (Sound Example "Streaming in the Galloping Rhythm Paradigm" <flag>). The galloping rhythm is generated by playing tones of two frequencies, let’s say 500 and 750 Hz, at a slow repetition rate in the pattern shown in the left side of figure 6.11. This is normally perceived as a simple “galloping” three-note melody (da di da – da di da – da di da …), as indicated at the left panel of the figure. If the melody is speeded up, however, or the frequency separation is increased, or, indeed, if you simply just keep listening to it for long enough, then the three-note melody breaks down and you perceive two streams of tones, one at the low frequency (da – da – da – da …), and a second, with larger gaps, at the high frequency (di – – – di – – – di …), as indicated in the right panel.

The breakdown of a sequence of sounds into two (or possibly more) things is called “streaming,” and we can talk about perception of one (at slower presentation rates) or two (at faster presentation rates) streams. Later, we will discuss the relationships between these things and auditory objects, which we introduced earlier in the chapter. The study of streaming was popularized by Al Bregman in the 1970s, and is described in great detail in his highly influential book Auditory Scene Analysis (Bregman, 1990). Importantly, the attempts of Bregman to justify the claim that there are multiple perceptual things, which he called streams, are described in that book and will not be repeated here.

Figure 6.12

The beginning of La Campanella etude from Liszt’s “Large Paganini Studies.” The melodic line consists of the low tones in the pianist’s right hand, which alternates with high tones, up to two octaves above the melodic line. The melody streams out in spite of the alternations with the high tones. The gray and black arrows indicate the notes participating in the two streams in one bar.

Streaming in this form has been used in classical music to create multiple musical lines with instruments that can produce only a single pitch at a time. The best known examples are probably from the Baroque period—for example, J. S. Bach in his compositions for solo violin famously used such melodies, composed of alternating high and low tones. These melodies split apart into two separate, simultaneous melodic lines, thus enriching the musical texture. Another rather well-known example is from Liszt’s La Campanella etude, which is a free adaptation of the main theme of the last movement of Paganini’s second violin concerto (figure 6.12 and Sound Example "La Campanella" on the book's Web site <flag>).

We have already mentioned that certain conditions, such as slow rhythms with long intervals and a small pitch separation between the notes, favor the perception of a single stream, while the opposite conditions, namely, fast presentation rates and large pitch intervals (as in the La Campanella etude), favor the perception of two separate streams. But what happens in ”intermediate” regimes? There is a tendency for the single stream to dominate perception for the first few seconds, following which the single percept may break up into two streams. Pressnitzer and Hupé (2006), who carefully measured the duration of this phase, found that for an interval of 5 semitones (the interval of a fourth, corresponding to a frequency ratio of about 4/3), and at a presentation rate of about 8 tones/s, the duration of the initial single-stream percept was on average about 20 s, corresponding to 160 tone presentations. Eventually, all subjects ended up hearing two streams. The eventual splitting of the initial single stream into two is called the “buildup of streaming.”

However, the story doesn’t end there. When subjects continued to listen to the sequences for even longer, the perceived organization could switch again into a single stream, and then split again, alternating between phases of one and two perceived streams. In fact, this behavior was very much the same as that found in other bistable perceptual phenomena (Pressnitzer & Hupé, 2006). Thus, the “buildup” of streaming, that is, the initial split, is only part of what neural models have to account for—it is also necessary to account for the further switching between the perception of one and two streams (Denham & Winkler, 2006).

Streaming occurs in nonhuman animals as well. Thus, MacDougall-Shackleton et al. (1998) showed streaming in a bird, the European starling, while Izumi (2002) observed an analog of streaming in Japanese macaques. In Izumi’s experiment, the monkeys had to recognize short “melodies” that were played alone or with additional interleaved distracter tones. If the distractor tones were positioned in a frequency region that did not overlap that of the melodies, the monkeys were able to recognize correctly the melodies. If the distracter tones were positioned in a frequency region that did overlap with that of the melodies, the monkeys failed to recognize the melodies.

The evidence for streaming in animals is, however, patchy. Human psychophysics is often compared directly with animal electrophysiological recordings, with the hope that the operation and organization of human and animal auditory systems are similar enough to make this comparison valid and informative. While such comparisons must be handled with care, they can nevertheless be illuminating. For example, a basic model for the mechanisms behind streaming was suggested by Fishman et al. (2001), based on recordings from the auditory cortex of macaques. The macaques listened passively to a sequence of two alternating tones (as in Sound Example "Streaming with Alternating Tones" <flag>), one of which matched the BF of the neurons under study. An example of the recorded neuronal responses is illustrated in figure 6.13, which shows the responses of two multiunit clusters to such sequences. The large, transient increases in firing rates (visible as peaks in the firing rate histograms) are the responses to the tones. The presentations of BF tones are marked by open dots and those of the non-BF tones by filled dots at the bottom of the panels (and by open arrows in the panels showing the responses to faster sequences). The crucial observation is that, as sequence rate is increased, the responses to the non-BF tones decrease faster than the responses to the BF tones. Thus, for example, at a presentation rate of 20 Hz, the BF tones evoke large responses in both of the recording sites shown, but the non-BF tone does not evoke any responses in one of them (the upper panel) and a substantially reduced response in the other (lower panel). Fishman et al. (2001) suggested that the differential effect of presentation rate on BF and non-BF tones is the result of “forward masking”—the reduction in response to a tone due to the presentation of another tone just before.

Figure 6.13

A possible neuronal correlate of streaming. The responses of two neurons to sequences of alternating tones presented at different rates. One of the two tones was always at BF, the other at an interval of 40% (top) or 50% (bottom) away. At the slower presentation rates, both tones evoked responses (e.g., the 5-Hz panels). However, at faster presentation rates, while the responses to both tones decreased, the responses to the non-BF tones decreased to a larger degree than those of the BF tone.

From figure 8 of Fishman et al. (2001).

How do these findings relate to streaming? Fishman et al. (2001) proposed the following hypothesis: As long as the majority of responsive neurons are activated by either of the two tones, a single stream is perceived. In contrast, if one tone evokes a response mostly in one neuronal population, while the other tone evokes a response mostly in a different, nonoverlapping neuronal population, two streams are perceived. Thus, when the frequency separation between the two tones is large enough, two streams are always perceived. Similarly, if the frequency separation between the two tones is very small, a single stream is always observed.

When the frequency separation between the two tones is intermediate, the rate of presentation becomes an important factor—slow presentations favor a single stream, because at low presentation rates there is less forward masking that would suppress responses to the non-BF tone. Increasing the presentation rate leads to more forward masking; in consequence, cortical neurons increasingly respond to only one tone or the other, but not to both. The neuronal populations responding to both tones tend to overlap less, which in turn favors the perception of the two tones in separate streams. The data of Fishman et al. (2001) are indeed compatible with this hypothesis.

This model is appealing, but it needs to be made quantitative. For example, one would like to know how much the two populations should overlap in order for a single stream to be perceived. Micheyl et al. (2005) used a nice twist to make this model quantitative. They decided to study the buildup of streaming—the time it takes for the initial galloping rhythm to split into two streams. First, they used ABA tone sequences at a fixed rate (8 tones/s) and measured (in humans, not macaques) which percept is present as a function of time. The results were as expected (figure 6.14B): When the interval between the two tones was 1 semitone (6%), for example, a single stream was almost always perceived, but when the interval was increased to 9 semitones, two streams were almost always heard. With 3- and 6-semitone separation, it took some time for the streams to separate, and there was some probability for hearing either one or two streams throughout the whole presentation period. Next, Micheyl et al. (2005) measured the responses of single neurons in the auditory cortex of macaque monkeys. They positioned the A tone on the BF of the neuron, so that the B tone was off-BF. Like Fishman et al. (2001), they observed a selective reduction in the response to the B tone, this time with increasing frequency separation. However, Micheyl et al. (2005) also studied how this reduction in the response to the off-BF tone (the B tone) developed with time, and found that the contrast between the responses to the A and B tones was stronger at the end than at the beginning of the sequence (figure 6.14A).

At this point, the decline in the response to the B tone mimics qualitatively the buildup of streaming, but Micheyl et al. (2005) went a step further. Remember that in this experiment, neurons always respond to the A tone, as that tone is at their BF. Micheyl and colleagues wanted to have a threshold such that if the neurons respond to the B tone above this threshold, they would also participate in the representation of the B tone and, according to the hypothesis of Fishman et al. (2001), there would be only one stream. On the other hand, when the response to the B tone is below the threshold, these neurons would not participate in the representation of the B tones, while other, similar neurons with a BF near the frequency of the B tone would presumably respond essentially only to the B tone. The A and the B tones would then be represented in the activity of nonoverlapping neural populations, which in turn should favor a two-stream percept.

How can we find such a threshold? Given a guess for the threshold, one can look back at the data and see how many times the responses to the B tone are smaller than that threshold—this would be an estimate for the probability of perceiving one streams rather than two. The question is, is it possible to find a single threshold that makes the predicted likelihoods of perceiving one stream, as derived from the neural recordings, line up with the actual likelihoods measured experimentally? The curves shown in figure 6.14B suggest that it is indeed possible to find such a threshold.

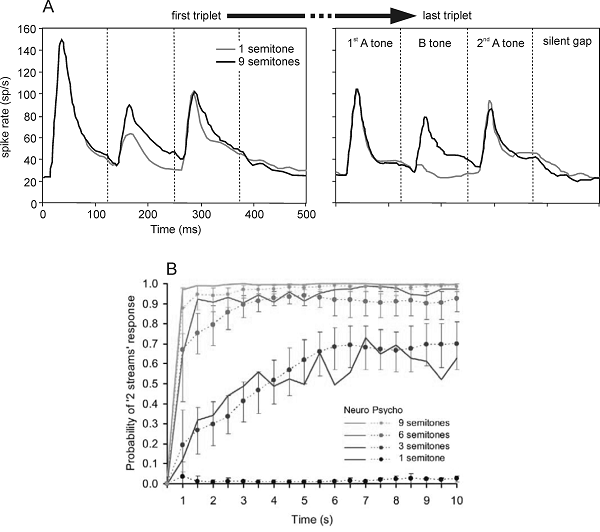
Figure 6.14

(A) Average responses of ninety-one neurons in the macaque auditory cortex to the ABA tone triplets, when the interval between the A and the B tones is 1 semitone (gray) and when the interval is 9 semitones (black). The responses to the first triplet are displayed on the left, and the responses to the last triplet on the right. Note the stronger reduction in the responses to the B tone in the 9 semitones case. (B) Buildup of streaming in humans (dashed lines) and in the neural model based on the responses in the macaque auditory cortex (continuous line).

From figures 2 and 4 of Micheyl et al. (2005).

These studies show that the dynamic response properties of cortical neurons may account for streaming, but they fall someway short of a conclusive and complete account of this phenomenon. A number of critiques and open questions are still to be answered. One critique states that, while this model accounts for the buildup, it doesn’t account for the bistability—the switching back and forth between one- and two-stream percepts. Unfortunately, no physiological study as yet even attempts to account for the bistability of streaming. A second critique is that, though this model may be correct, it doesn’t necessarily have to be based on cortical responses. In fact, neurons as early as the cochlear nucleus show a similar, although substantially smaller, differential adaptation effect. The effect is smaller, but the variability in the responses in the cochlear nucleus is also much smaller, and therefore the same statistical technique used to produce the fit between monkey cortical responses and human behavior can produce a similar fit between the responses of neurons in the cochlear nucleus of the guinea pig and human behavior (Pressnitzer et al., 2008). As we have seen so often in this chapter, high-level and low-level mechanisms compete for explaining the same perceptual phenomena.

A third critique is that the Fishman model has been studied only for streaming based on frequency differences. However, streaming can be induced by many acoustic differences—for example, by amplitude modulation rate, which is only very weakly related to spectral differences (Sound Example "Streaming by Amplitude Modulation Rate" on the book's Web site <flag>). Whether the same type of increased differentiation between populations would occur for other acoustic differences is an open question. Some initial work in this direction shows a possibility to generalize the Fishman model to amplitude modulation (Itatani & Klump, 2009).

With the recent intensive research into streaming, the “playground” for relating it to neural responses is now well delimited. To hazard a guess, the main weakness of all models today is their inability to account for bistability. Thus, many puzzles remain for future work, and possibly for new conceptual models as well.

6.5 Nonsimultaneous Grouping and Segregation: Change Detection

You sit in a room preparing for an exam that is going to take place tomorrow. Music is playing in the background. Through the windows, sounds from the busy street are heard. Your roommate is walking in the next room, stepping from one end of the room to the other, but you ignore all of these sounds, concentrating on your revision. Then one of your friend’s steps is different—and you are suddenly aware of it.

As we discussed in the first chapter, sounds provide information about numerous aspects of the world, and minute changes in sounds, such as the sound of a step on a different material than we expected, may be highly informative. We are very sensitive to such changes in the auditory scene. This sensitivity is often studied with a tool called Mismatch Negativity (MMN). MMN is a component of the so-called auditory event-related potentials (ERPs), the set of electrical waves that are evoked by sounds and measured by electroencephalography (EEG).

MMN is evoked by unexpected sounds embedded in a stream of expected sounds. It is preattentive: evoked even without attention. In the simplest version of an experiment for measuring MMN, the subject is distracted (e.g., by reading a book or watching a silent movie) while sounds are played by earphones and the EEG is measured. The sound sequence usually consists of two pure tones that vary in some property: They may have different frequencies, or different sound levels, or different durations. One of the two tones is played with high probability (this tone is often called the standard), while the other is rare (the deviant). The deviant tone is presented randomly in the sequence, for example, with a probability of 10%. Under these circumstances, the ERP is somewhat different in response to the standard and to the deviant: When measuring the potential between the top of the head and the bottom of the mastoids, the response to the deviant is more negative than the response to the standard in a time window around 100 to 150 ms after stimulus onset (figure 6.15).

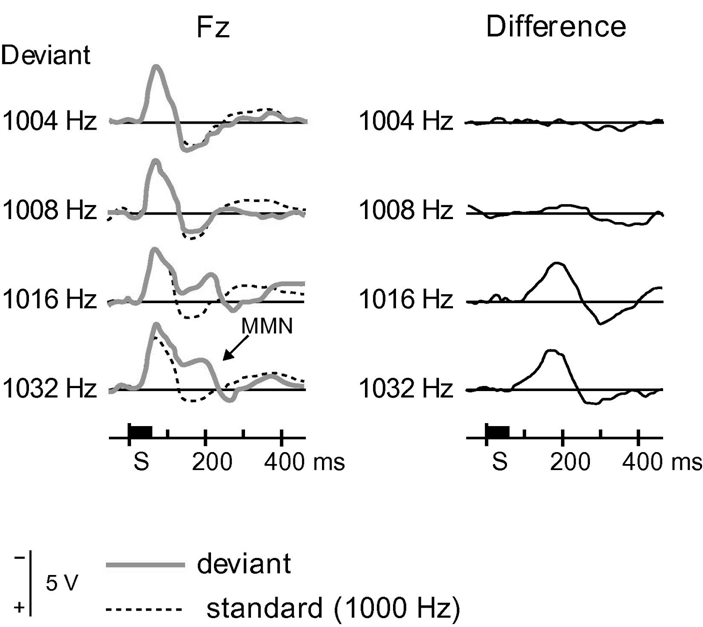
Figure 6.15

Mismatch negativity (MMN) to frequency deviants. (Left) The potential between electrode Fz (an electrode on the midline, relatively frontal) and the mastoid in response to a 1,000-Hz tone (dashed line) that serves as the standard, and deviant tones at the indicated frequencies. (Right) The difference waveforms (deviant-standard), showing a clear peak around 150 ms after stimulus onset. Note that negative potentials are plotted upward in this figure.

From figure 1 of Naatanen et al. (2007).

MMN can be observed even when the changes in the sounds are quite subtle. It is sensitive to conjunction of properties or even to deviations from rather complex rules that might govern the stimulation sequence. In one of the more complex designs that have been tested, Paavilainen, Arajarvi, and Takegata (2007) used a sequence that could have tones of two frequencies, and these tones were either short or long. Each of the four possible combinations of tone frequency and tone duration (high-long, high-short, low-long, and low-short) appeared with equal probability. However, the sequence (Sound Example "A Tone Sequence Following a Complex Rule" on the book's Web site <flag>) was constructed so that short tones were almost always followed by low-frequency tones (which could be either long or short), and long tones were always followed by high-frequency tones (which also could be either long or short). From time to time, a tone appeared that violated these rules (a high-frequency tone followed a short tone, or a low-frequency tone followed a long tone). These deviant tones evoked MMN (admittedly, a rather small one). Remarkably, in interviews following the experiment, the listeners reported that they were not aware of the rules governing the sequence, nor were they able to work out what the rules were when prompted, and when the rule was explained to them, they had great difficulty applying it to detect deviants through a conscious effort. Thus, the MMN stemmed from a presumably preattentive representation of the regularities in the sound sequence.

But what can these laboratory experiments tell us about real-world listening? Going back to the situation described at the beginning of this section, would our friend’s deviant footstep evoke MMN? Apparently it does. Winkler and coworkers (2003) measured MMN in subjects who watched a movie (with sound), and were simultaneously presented with simulated street sounds. On top of this, the sounds of eleven footsteps were heard. The sounds of the steps varied a bit from one step to the next, as real steps would. One of the steps simulated walking on a different surface, and this was inserted either as the second or tenth in the sequence (Sound Example "A Naturalistic Sound Sequence with a Deviant" on the book's Web site <flag>). The subjects were engaged in a task that was related to the movie, and so they had to ignore the other two sound sources. Winkler et al. (2003) found that MMN was evoked when the deviant step was the tenth but not when it was the second in the sequence. Thus, MMN was evoked in spite of the natural variability in the sounds—presumably, when the deviant step was the tenth, a representation of the regularity of the footsteps had been generated during the preceding nine steps, so that the deviant step was detected as such. On the other hand, when the deviant step was in the second position, no representation of regularity could have been created, and no MMN occurred.

What do we know about the brain activity underlying MMN? Since MMN was defined and intensively studied in humans, while more fine-grained studies, such a single-neuron recordings, can usually be conducted only in nonhuman animals, it is necessary to show that MMN, or something similar, occurs in animals. And indeed, a number of studies that measured auditory evoked potentials in rats (Ruusuvirta, Penttonen, & Korhonen, 1998), cats (Csepe, Karmos, & Molnar, 1987), and monkeys (Javitt et al., 1992) reported brain responses that are similar to MMN. These results open the road to single neuron studies.

The single-neuron analogs of MMN are based on a phenomenon that has been studied in vision for some time, but was only recently imported into auditory research—stimulus-specific adaptation (SSA). We start with two stimuli, both of which evoke responses of similar strength. Next, we present one of the two stimuli repeatedly, causing a reduction in the response (adaptation). Finally, we present the other stimulus. It is possible that the neuron is really tired of responding—in that case, the response to the other stimulus would be adapted as well. However, in many cases, the response to the other stimulus is not adapted at all, or only partially adapted. In that case, we will say that the adaptation to the first stimulus is stimulus specific, or that we have SSA.

SSA is interesting, precisely because it is not really adaptation, which is usually defined as a use-dependent reduction in responses. If adaptation were really a kind of use-dependent “fatigue,” then the decline in the neuron’s ability to respond vigorously should affect all stimuli more or less equally. In stimulus-specific adaptation, the neuron has tired only of the repetitive, adapting stimulus, but can still fire vigorously to a different, rare stimulus. A better term would have been “habituation,” which is used in the psychological literature to indicate a reduction in responses that may be stimulus specific (Dudai, 2002).

It turns out that SSA is strong in the auditory midbrain and cortex. Ulanovsky et al. (2003) used oddball sequences of pure tones, similar to those used in MMN research, and recorded single-unit responses in auditory cortex of cats. To demonstrate stimulus-specific adaptation, they used two tones that were very close in frequency—to within 10% or even 4%, which is the behavioral limit of frequency discrimination in cats. They then played one of the tones as standard with the other as deviant. As expected, the neurons adapted to the repetitive standard tone, and the deviant tone evoked relatively larger responses. However, how do we know that the neuron does not have larger responses to the deviant tone because of preference for its frequency (it might be closer to the neuron’s BF than the standard), rather than any adaptive effects? Ulanovsky et al. (2003) controlled for this issue by repeating the experiment with the roles of the standard and the deviant reversed. Since both tones served once as standard and once deviant, any intrinsic preference for one of the tone frequencies could be discounted. Some of their results are presented in figure 6.16. The responses to a tone when it was standard (thick light gray line) were most often smaller than the responses to the same tone when it was deviant (thick dark gray line). Thus, the neuron was sensitive to the statistical structure of the sequence, producing larger responses to rare sounds.

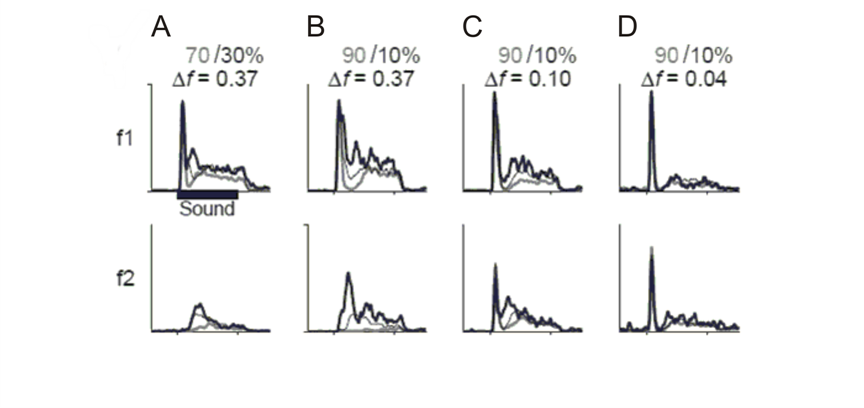
Figure 6.16

Responses of a neuron in cat auditory cortex to two frequencies (f1 and f2). The frequency difference between the tones is given at the top of each column, as well as the probabilities of the two tones. The responses are displayed as peristimulus time histograms, computed by averaging all the responses to the given frequency under three conditions: when rare (thick black line), when common (thick gray line), and when appearing randomly half the time (thin gray line).

From figure 1 in Ulanovsky, Las, and Nelken, (2003).

 

 [DH1]Au: Please add to References.

ELN: DONE.

Although the original observations of Ulanovsky et al. (2003) suggested that SSA occurs in primary auditory cortex but not in the thalamus, and would therefore be a result of cortical mechanisms, it is clear today that the situation is much more complex. SSA has since been observed already in inferior colliculus (Malmierca et al., 2009), although it is strong and widespread mostly outside the core station of the inferior colliculus, the central nucleus. Similarly, SSA has been observed in the medial geniculate body of the thalamus (Anderson, Christianson, & Linden, 2009), although there, too, it is strongest outside the core division. Within auditory cortex, SSA appears to be more pronounced in the deeper, infragranular layers, which suggests that cortical processing may amplify it (Szymanski, Garcia-Lazaro, & Schnupp, 2009). The precise contributions of midbrain and cortical stations to the phenomenon of SSA remain to be worked out.

Is SSA the “single-neural correlate” of MMN? A number of observations suggest that the relationship between MMN and SSA is indirect. MMN occurs rather late compared to the neural responses that are usually studied in single-neuron experiments. Sometimes MMN occurs with latencies of 150 ms after stimulus onset in humans, whereas the earliest cortical responses in humans occur within 30 ms after stimulus onset (Schneider et al., 2002), and SSA is present right from the onset of the response. This temporal mismatch suggests that, in humans, too, there should be a neural signature of early deviance detection. More important, the fact that SSA in single neurons occurs so much earlier than MMN, raises the possibility that it may occur, in a sense, “upstream” of MMN, and trigger a further cascade of neural processing events that ultimately produce the currents measured as MMN.

Although the relationships between SSA and MMN remains uncertain, it is clear that both share a large number of properties (Nelken & Ulanovsky, 2007) that are important for auditory scene analysis—most important, the sensitivity to sudden, unpredictable changes in the auditory scene. Thus, the auditory system comes equipped with deviance detectors, which may signal when the mental image we have created in the auditory scene needs to be updated.

6.6 Summary: Auditory Scene Analysis and Auditory Objects

Grouping and segregating multiple simultaneous and sequential sound elements to form either unified or separate “perceptual objects” is one of the most important computational tasks the auditory system performs. This task underpins, for example, our ability to understand speech under the usual adverse conditions of daily life, with competing sources and noise all around. It underpins music appreciation, particularly once we go beyond a single instrument playing a single melody. It also underlies our ability to detect subtle changes in the auditory scene, with its obvious ethological implications.

In our discussion, we referred to the formation of ”auditory objects” as the result of auditory scene analysis, but also pointed out that there is as yet no consensus as to how auditory objects are to be defined. We encountered the term first in discussing masking—in that scenario, there are presumably two “things,” the masker (usually some noise) and the target sound that is being masked (usually a pure tone). When we discussed simultaneous grouping and segregation, we again dealt with two things, such as two simultaneously present vowels that differ in F0, or a vowel and a lonely harmonic that had become separated from the vowel because it started a bit early. The role of the auditory system was presumably to realize the distinction between these temporally overlapping sounds, putting bits of sounds in two baskets, one for each, well, “thing.” Streaming has a similar flavor—you put the successive tones in a single stream or in two separate streams. However, when we called these things “streams,” rather than baskets or objects, we were following historical convention, not applying any precise or agreed-upon definitions or distinctions. So, what are these things (objects, baskets)?

One thing they are definitely not is “sounds” in the physical sense, because there is only one sound at each moment in time—the physical pressure waveform that causes the tympanic membrane to vibrate. When we call these things sounds in the perceptual sense, as in “I heard two sounds, one of them a pure tone and the other noise,” we really mean that we have somewhere in our head the idea that the physical sound we just experienced appeared to be formed by adding these individual “things” together.

It is also a bit of stretch to call these things “sound sources.” They will often carry information about the sound sources, but the relationships between sound sources and the sound they emit is far from being one-to-one—when I listen to a recording of a Mahler symphony, the sound source is a loudspeaker, but the sounds I perceive are the instruments of the orchestra, alone or in combination. Classical composers perfected the art of combining different instruments together to achieve sonorities and textures that cannot be achieved by single instruments, so that multiple sound sources may appear to fuse into a single “thing.” Or consider the fact that animals are sound sources that can produce very different vocalizations. Think of a cat meowing, purring, or hissing. Is the auditory object a “meow,” or is it a cat?

Referring to the perceived auditory things we discussed in this chapter as “events” is also problematic. An event suggests localization in time, but the things can be rather long lasting, and they may even appear and disappear from our perception, as we have seen in the case of the bistable percept of streaming.

According to Bregman, the main importance of these things is that they serve as carriers of properties—which is precisely the purpose of objects in vision. Thus, the auditory thing may have a pitch (or not), it may have a spatial location, or it may have a phonetic quality (or not). It may have a long or short duration, be continuous or transient or rhythmic, and so on and so forth. In that respect, one might define an auditory object, as a carrier of properties: a “thing” that has a specific set of values for all of these perceptual properties.

Bregman himself preferred to call these things streams, and stated that The “stream plays the same role in auditory mental experience as the object does in visual [mental experience]” (Bregman, 1990, p. 11). The term “stream” has been recently used mostly in the context of streaming—the splitting of the two-tone sequences into two streams. It has therefore acquired a more specific sense than Bregman seems to have intended originally. One could say that a stream is an auditory object, but in current usage there are auditory objects that are not streams—for example, a single burst of white noise over a background of silence wouldn’t be a stream, according to current terminology.

There have been a number of attempts to define auditory objects in more precise terms. For example, an influential review of Griffiths and Warren (2004) suggested four principles for defining auditory objects. Auditory objects should pertain to things in the sensory world; object analysis is about separating information related to the object and that related to the rest of the world; it should involve abstraction of sensory information, so that different physical realizations may evoke the same auditory object; and finally it should generalize across senses (so that the voice and picture of grandma should represent the same object).

This definition is substantially more restrictive than the arguments we used (and that Bregman used before us) would require. While our rough discussion is consistent with the first two postulates of Griffiths and Warren, it certainly doesn’t go as far as requiring the last two. The “things” we discuss do not necessarily have any specific relationships to material objects—they are auditory, and have to do with the sounds and not with what produced the sounds. They may represent an earlier or more primitive representation relative to the objects, as defined by Griffiths and Warren.

What does perhaps become clear in this discussion is that the vocabulary of the English language is at present not adequate to discuss the process of “auditory object formation,” and we may have to invent, or borrow, new vocabulary to create the necessary clarity. In German, for example, the word schall is used exclusively for physical sound, while sound in the perceptual sense is called a geräusch or a klang. But the word “klang” would not be used to describe a stream. Rather, a stream is composed of a succession of perceptually linked “klänge.” The lower-level, “klang-object” is more unitary, more strongly bound perceptually. We would find it much easier to report how many klänge there were in a stream, than to guess how many harmonics there were in a klang, even if all the harmonics were resolved by the cochlear filters.

As this discussion illustrates, while auditory objects may have many meanings, these things clearly have an important place in auditory research, as they lie right at the interface between physiology and perception. In particular, we want to argue that objects (in the sense of an entity with a particular set of perceptual properties) must be formed before they are assigned properties such as pitch, spatial location, phonetic quality, and so on. This point was made more or less explicitly throughout this chapter. For example, the models we described for separating vowels in double-vowel experiments consisted of a stage in which different frequency channels that shared similar periodicity were grouped together, and only later could the phonetic quality in each group be assigned. Throughout the chapter we reviewed evidence to suggest that the “klang-objects” are already encoded in primary auditory cortex. We also reviewed evidence suggesting that the neural mechanisms that underlie streaming are expressed in primary auditory cortex, and possibly even in the cochlear nucleus. Thus, it seems that the construction of the auditory objects begins remarkably early in the auditory system, presumably in parallel with feature extraction. These findings can be contrasted with the difficulty in finding early representations of pitch (or even just a representation of periodicity, as reviewed in chapter 3), space (as reviewed in chapter 5), and speech sound identity (as reviewed in chapter 4). Taken together, these electrophysiological findings may support the contention that objects are formed before their properties are assigned to them.

How can the brain find out about the objects in the auditory scene? The examples for auditory scene analysis that we have considered all revolved around rules that help us assign different frequency components or sound elements to different objects. The rules included grouping by common onset across frequency, or grouping by common periodicity, (klang formation) or segregating elements that are too far in frequency and too close in time (for streaming). We also saw that our auditory system is very sensitive to statistical regularities, and their violation gives rise to MMN. Thus, it is tempting to argue that objects embody such grouping and regularity rules. According to this circle of ideas, as long as the rules defining the object describe the auditory scene well, we perceive the object; once these rules are violated, we can either introduce a new object into the scene (something Bregman called the old plus new heuristic), or, if this is not a good solution, completely turn off the object—and cease to perceive it (see Winkler et al., 2009a, for a detailed presentation of these ideas).

Thus, we are left in a precarious state—we have a number of well-studied examples of auditory scene analysis, some loose terminology for describing its outcome (the formation of auditory objects), and a very rough suggestion for how this may be achieved (by finding and applying the rules that bind or separate the elements of the current auditory scene). All of this leaves a lot of room for further research, which will need to integrate electrophysiology, perception, and modeling—a perfect mix for fascinating new findings!